PROBLEMS ON DIAGONALS OF 2D SHAPES

Problem 1 :

If the diagonal of a rectangle is 17 cm long and its perimeter is 46 cm, find the area of the rectangle.

Solution :

Let Length = x and width = y

Length of the diagonal = 17 cm

x² + y² = 17²

x² + y² = 289 ----(1)

Perimeter of the rectangle = 46 cm

2(x + y) = 46

Dividing by 2, we get

x + y = 23

Using the algebraic identity

a² + b² = (a + b)² - 2ab

x² + y² = (x + y)² - 2xy

Applying x² + y² in (1), we get

x² + y² = 289

(x + y)² - 2xy = 289

23² - 2xy = 289

529 - 289 = 2xy

240 = 2xy

xy = 120

So, area of the rectangle is 120 cm².

Problem 2 :

One side of the rectangular field is 15 m and one of its diagonal is 17 m. Find the area of the field.

Solution :

Length and width be the dimensions of the rectangle.

(Length)² + (width)² = (diagonal)²

Let length = 15 m

(15)² + (width)² = 17²

225 + (width)² = 289

(width)² = 289 - 225

Width = √64

width = 8 m

Area of the rectangle = 15(8)

= 120 m²

Problem 3 :

Find the area of square, one of whose diagonals is 3.8 m long.

Solution :

Since it is square, length of all sides will be equal.

a² + a² = (3.8)²

2a² = 14.44

a² = 7.22

So, area of the square is 7.22 m²

Problem 4 :

Find the area of a rhombus one side of which measures 20 cm and one diagonal 24 cm.

Solution :

In rhombus, the diagonals will bisect each other at right angle

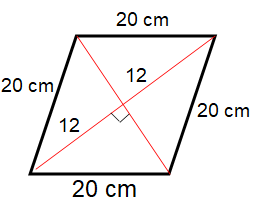
Let 2x be the length of the another diagonal. So, x be its half length.

12² + x² = 20²

144 + x² = 400

x² = 400 - 144

x² = 256

x = √256

x = 16 cm

Area of rhombus = (1/2) ⋅ 32 ⋅ 24

= 384 cm²

Problem 5 :

One diagonal of a parallelogram is 70 cm and the perpendicular distance of this diagonal from either of the outlying vertices is 27 cm. The area of the parallelogram is.

Solution :

The diagonal will divide the parallelogram into two triangles of equal area.

Base of the triangle = 70 cm

height of the triangle = 27 cm

Area of one triangle =  (1/2) ⋅ 70 ⋅ 27

= 945 cm²

Area of parallelogram = 2(945)

= 1800 cm²