PROBLEMS ON CONSTRUCTING MODELS IN SAT

Problem 1 :

Last Saturday, Maya drove from her house to the bookstore, where she stayed for several hours before driving back home. Which of the following graphs could represent Maya's trip ?

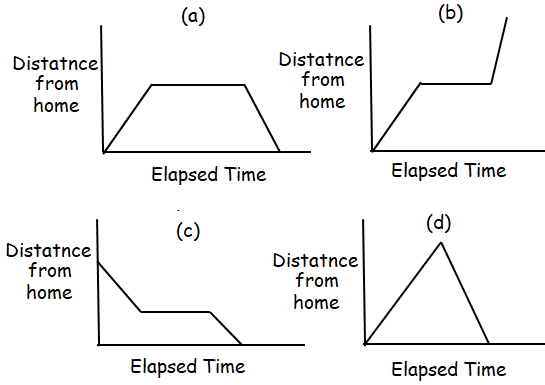
Solution :

Work done by Maya :

Work 1 :

Maya drove from her house to the bookstore

Work 2 :

She stayed for several hours

Work 3 :

Returning back to home.

Option a suits the situation.

Problem 2 :

At a movie theater, an adult ticket costs $10 and a bag of popcorn costs $6. If a group of adults bought tickets to a movie and 4 bags of popcorn, what expression could be used to determine how much in total the group spent, in dollars ?

(a)  10x + 6, where x is the number of adults

(b)  10x + 24, where x is the number of adults

(c)  16x, where x is the number of adults

(d)  6x + 10, where x is the number of bags of popcorn purchased.

Solution :

Let x be the number of adults.

Cost of 1 adult ticket = x

Cost of 1 bag of popcorn = $6

Cost of 4 bags of popcorn = 4(6) = 24

Total cost = 10x + 24

Problem 3 :

On Friday, Janice read x pages every 30 minutes for 4 hours, and Kim read y pages every 15 minutes for 5 hours. Which of the following represents the total number of pages read by Janice and Kim on Friday ?

(a)  4x + 5y     (b)  8x + 20y     (c)  20x + 8y    (d)  120x + 75y

Solution :

Number of 30 minutes interval in 4 hours = 8

Number of 15 minutes interval in 5 hours = 20

So, the answer is 8x + 20y

Problem 4 :

At the start of a semester, 150 students enroll in a course for which the regular tuition fee is $5, 400. The school finds that for every $200 discounts on the tuition fee for the course, the students enrollment increase by 9. Which of the following equation gives the student enrollment E when the tuition fee for the course is discounted by d dollars ?

(a)  E = 150 + 0.045 d        (b)  E = 150 + 9d

(c)  E = 150+0.045(5400 - d)    (d)  E = 150+9(5400 - 200d)

Solution :

For every 200 discount, 9 students increases.

Rate of increment = 9d/200

Initial enrollment with no discount = 150

total enrollment = 150 + (9d/200)

E = 150 + 0.045 d

Problem 5 :

Jones climbed a mountain at the speed of 1 kilometer per hour and came down at the speed of 2 kilometer per hour. Which of the following could be the graph of the distance from the bottom of the mountain as a function of time ?

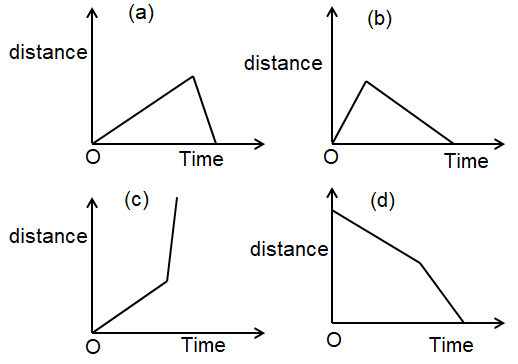
Solution :

Since Jones starts at the bottom of the mountain and ends up at the bottom, the correct graph must start at the x-axis and return to the x-axis. Only graph (a) and (b) do that.

Jones comes down at twice the speed, the later portion of the graph should be steeper than the initial portion. So, graph (a) is the answer.

Problem 6 :

Kevin has collected m coins. Ellie has collected half as many as Kevin, but 5 more than Robert. In terms of m, how many coins has Robert collected ?

(a)  2m - 5    (b) (m/2) + 5     (c)  2m + 5    (d)  (m/2) - 5

Solution :

Number of coins collected by Kevin = m

Number of coins collected by Ellie = m/2

But Ellie has 5 more than Robert, then Robert will have 5 less than Ellie has.

Number of coins collected by Robert = (m/2) - 5. So, option d.

Problem 7 :

A clothing company sells its flagship winter jacket all year round. The table above shows the quantity demanded when the price of the jacket is $320 and when it is $360. Assuming the quantity demanded decrease at a constant rate with respect to price, which of the following linear functions Q best models the quantity demanded when the price of the jacket p in dollars ?

(a)  Q(p) = 93600 - 235p     (b)  Q(p) = 93600 - 260p

(c)  Q(p) = 93600 - 235(p - 320)

(d)  Q(p) = 93600 - 260(p - 320)

Solution :

From the information, it is clear the quantity demanded decrease at the constant rate.

(320, 93600) and (360, 84200)

Creating linear model, we get

Q(p) = 93600 - 235p 

So, option a.

Problem 8 :

A movie rental service charges $15 as a monthly subscription fee and $3 per movie rented. If Alex rents x movies per month from this service, which of the following expression gives the total amount in dollars, he spends on movie rentals in one year ?

(a) 12(18x)   (b)  15 + 12(3x)

(c)  12(15) + 3x   (d) 12 (15 + 3x)

Solution :

Year consists of 12 months, for 1 movie he spends rent as $3.

x be the number of movies he is seeing.

Then,

total amount =

Number of months per year (monthly subscription + 3x)

= 12(15 + 3x)

So, option d.

Problem 9 :

A car has an estimated initial value of $65000. Once the car is sold, its value decreases at a constant rate of $2300 per year. Which of the following equations best approximated the value V in dollars, of the car t years after it is sold, for 0 ≤ t ≤ 28 ?

(a)  V = 65000 + 2800t    (b)  V = 65000 - 2800t

(c)  V = 65000 + 2300t   (d)  V = 65000 - 2300t

Solution :

Initial value = 65000 

Decreases at the rate of $2300, so -2300

Creating model, we get

V = 65000 - 2300t

Problem 10 :

A grocery store uses crates to store a total of 36a apples and 24w watermelons. Each crate can be used to store either 12 apples or 6 watermelons. Which of the following expression gives the total number of crates the grocery store uses to store apples and watermelons.

(a) 3a + 4w    (b)  4a + 3w    (c) 1/4a + 1/3w    (d)  1/3a + 1/4w

Solution :

Quantity of apples = 36a

Quantity of watermelons = 24w

number of crates = (36a/12) + (24w/6)

= 3a + 4w