PROBLEMS ON CHORD TANGENT AND RADIUS OF A CIRCLE

Problem 1 :

In the figure given below, point E is the center and m∠CED = 55°. What is the area of the circle?

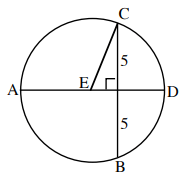
Solution :

Let F be the point of intersection of chords AD and CB.

In triangle EFC,

sin θ = Opposite side / Hypotenuse

sin 55 = FC / EC

0.819 = 5 / EC

EC = 5 / 0.819

EC = 6.10

Radius of the circle = 6.10

Area of the circle =  π r²

= 3.14 (6.10)²

= 116.83 cm²

Problem 2 :

In the following problems, B is the center of the circle. Find the length of BF given the lengths below. 

i)  EC = 14, AB = 16

ii)  FD = 5, EF = 10

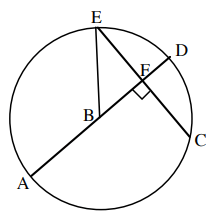
Solution :

BF is the perpendicular drawn to the chord EC. It should be a perpendicular bisector. So, EF = 7

In triangle EFB,

AB = BE

BE² = BF² + FE²

16² = 7² + FE²

256 = 49 + FE²

FE² = 256 - 49

FE² = 207

EF = √207

EF = 14.38

ii)  FD = 5, EF = 10

BD is the radius of the circle, BD = BF + FD

BD = BF + 5

BF = BD - 5

BE = AB = BD = r

BF = r - 5

BE² = BF² + FE²

r² = (r - 5)² + 10²

r² = r² - 10 r + 25 + 100

10r = 125

r = 12.5

BF = 12.5 - 5 ==> 7.5

Problem 3 :

In J, radius JL and chord MN have lengths of 10 cm. Find the distance from J to MN .

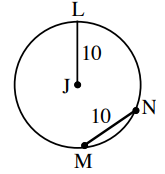
Solution :

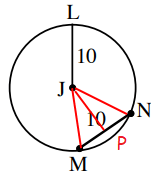
In triangle JNP,

JN² = JP² + PN²

10² = JP² + 5²

100 - 25 = JP²

JP² = 75

JP = √75

JP = 5√3

So, the distance J and MN is 5√3.

Problem 4 :

In the circle O is the center, OC = 13 and OT = 5. Find AB.

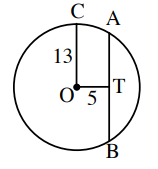
Solution :

Connecting OA,

OA² = OT² + TA²

OA and OC are radii.

13² = 5² + TA²

AT²= 169 - 25

AT²= 144

AT = 12