PROBLEMS ON CENTROID OF TRIANGLE

• The centroid R of a triangle is two thirds of the distance from each vertex to the midpoint of the opposite side.

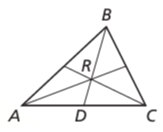
BR = (2/3) BD

• The median of a triangle is a line segment joining the vertex of the triangle to the mid-point of its opposite side.
• It bisects the opposite side, dividing it into two equal parts.
• The median of a triangle further divides the triangle into two triangles having the same area.

Problem 1 :

In ABC shown below, P is the centroid and BF = 18

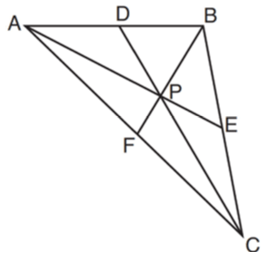
What is the length of BP?

1) 6         2) 9       3) 3        4) 12

Solution :

BP = 2/3 of BF

BP = (2/3) x 18

= 2 x 6

= 12

So, length of BP is 12 units.

Problem 2 :

In the diagram below, point P is the centroid of ABC

If PM = 2x + 5 and BP = 7x + 4, what is the length of PM?

1) 9     2) 2      3) 18      4) 27

Solution :

BP : PM = 2 : 1

(7x + 4) : (2x + 5) = 2 : 1

(7x + 4)/(2x + 5) = 2/1

7x + 4 = 2(2x + 5)

7x + 4 = 4x + 10

7x - 4x = 10 - 4

3x = 6

x = 6/3

x = 2

PM = 2x + 5

= 2(2) + 5

= 4 + 5

PM = 9 units.

Problem 3 :

In the diagram below, QM is a median of triangle PQR and point C is the centroid of triangle PQR.

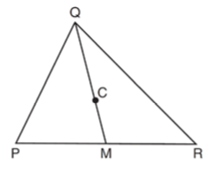
If QC = 5x and CM = x + 12, determine and state the length of QM.

Solution :

QC : CM = 2 : 1

5x : (x + 12) = 2 : 1

5x / (x + 12) = 2/1

5x = 2(x + 12)

5x = 2x + 24

5x - 2x = 24

3x = 24

x = 24/3

x = 8

QM = QC + CM

= 5x + x + 12

= 6x + 12

= 6(8) + 12

= 48 + 12

QM = 60

So, the length of QM is 60 units.

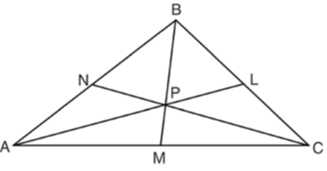
Problem 4 :

In XYZ, shown below, medians XE, YF, and ZD intersect at C.

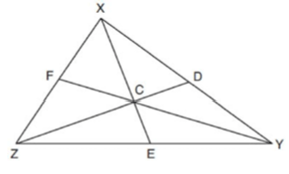
If CE = 5, YF = 21, and XZ = 15, determine and state the perimeter of triangle CFX.

Solution :

Perimeter of triangle CFX = CF + CX + FX --------(1)

EX = CE + CX

EX = 5 + (2/3) of EX

EX - (2/3) of EX = 5

1/3 of EX = 5

EX = 5(3)

EX = 15

CX = (2/3) of 15

= (2/3) ⋅ 15

= 2(5)

CX = 10

XZ = 15

FX = 15/2 ==> 7.5

YF = 21

CF = 1/3 of YF

= (1/3) x 21

CF = 7

Perimeter of triangle CFX = 7 + 10 + 7.5

= 24.5 units

Problem 5 :

Point D is the centroid of △ABC. Use the given information to find the value of x

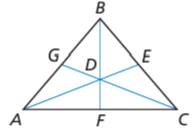
(i)  BD = 4x + 5 and BF = 9x

(ii)  GD = 2x − 8 and GC = 3x + 3

(iii)  AD = 5x and DE = 3x − 2

(iv)  DF = 4x − 1 and BD = 6x + 4

Solution :

BD : DF = 2 : 1

BF = BD + DF

9x = 4x + 5 + DF

9x - 4x - 5 = DF

DF = 5x - 5

(4x + 5) : (5x - 5) = 2 : 1

(4x + 5) / (5x - 5) = 2/1

4x + 5 = 2(5x - 5)

4x + 5 = 10x - 10

4x - 10x = -10 - 5

-6x = -15

x = 15/6

x = 5/2

So, the value of x is 2.5 units.

(ii)  GD = 2x − 8 and GC = 3x + 3

GD = (1/3) of GC

= (1/3) ⋅ (3x + 3)

= x + 1

From the given information, GD = 2x - 8

2x - 8 = x + 1

2x - x = 1 + 8

x = 9

So, the value of x is 9 units.

(iii)  AD = 5x and DE = 3x − 2

AD = (2/3) of AE

AE = AD + DE

= 5x + 3x - 2

= 8x - 2

Applying the value of AE, we get

AD = (2/3) (8x - 2)

5x = (2/3) (8x - 2)

3(5x) = 2(8x - 2)

15x = 16x - 4

15x - 16x = -4

-x = -4

x = 4

So, the value of x is 4 units.

(iv)  DF = 4x − 1 and BD = 6x + 4

BD + DF = BF

6x + 4 + 4x - 1 = BF

BF = 10x + 3

DF = (1/3) of BF

4x - 1 = (1/3) of 10x + 3

3(4x - 1) = 1(10x + 3)

12x - 3 = 10x + 3

12x - 10x = 3 + 3

2x = 6

x = 6/2

x = 3

So, the value of x is 3 units.