PROBLEMS ON CENTRAL ANGLE CREATED BY TWO RADIUS OF THE CIRCLE

Problem 1 :

Find the angles marked with letters in each of the following diagrams, if O is the center of the circle.

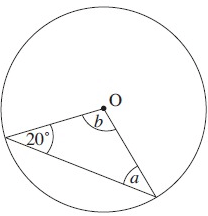
Solution :

By observing the figure. O is the center of the circle. It is a isosceles triangle.

a = 20^º

20^º + b + 20^º = 180^º

40^º + b = 180^º

b = 180^º – 40^º

b = 140^º

So, the values  of a is 20^º, b is 140^º.

Problem 2 :

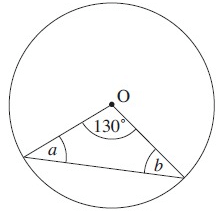
Solution :

By observing the figure. It is a isosceles triangle.

a + b + 130^º = 180^º

b = a

a + a + 130^º = 180^º

2a = 180^º - 130^º

2a = 50^º

a = 50^º/2

a = 25^º

So, the values of a is 25^º, b is 25^º.

Problem 3 :

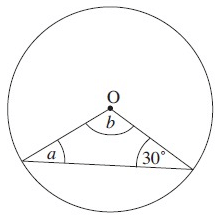
Solution :

By observing the figure. O is the center of the circle. It is a isosceles triangle.

a = 30^º

30^º + b + 30^º = 180^º

60^º + b = 180^º

b = 180^º – 60^º

b = 120^º

So, the values of a is 30^º, b is 120^º.

Problem 4 :

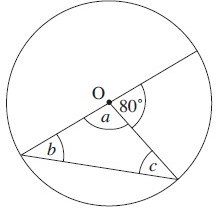
Solution :

a + 80^º = 180

a = 180 - 80

a = 100^º

b = c

a + b + c = 180^º

100^º + c + c = 180^º

100^º + 2c = 180 ^º

2c = 180 – 100

2c = 80

Diving 2 on both sides.

c = 40

So, the values of a is10cal0^º, b = c = 40^º.

Problem 5 :

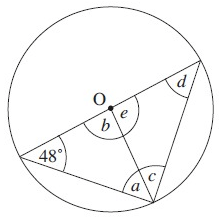
Solution :

By observing the figure,

e + c + d = 180

96 + c + c = 180

96 + 2c = 180

2c = 180 - 96

2c = 84

c = 84/2

c = 42

So, the values of a = 48, b = 84^º, c = d = 42^º, e = 6 ^º.

Problem 6 :

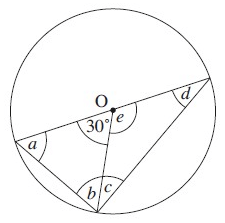
Solution :

By observing the figure,

e + c + d = 180

c = d

150 + c + c = 180

150 + 2c = 180

2c = 180 - 150

2c = 30

c = 15

So, the values of a = b = 75^º, c = d = 55^º, e = 60 ^º.

Problem 7 : 

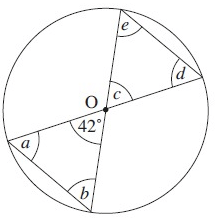
Solution :

By observing the figure.

So, the values of a = b = 69^º, c = 42^º, e = d = 69 ^º.

Problem 8 :

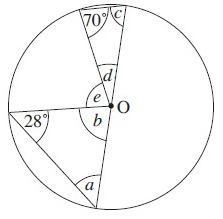
Solution :

By observing the figure.

b + e + d = 180

124 + e + 40 = 180

164 + e = 180

e = 180 - 164

e = 16

So, the values of a = 28^º, b = 124^º, c = 70^º, d = 40^º, e = 16^º.