PROBLEMS ON AREA RELATED TO CIRCLES CLASS 10

Problem 1 :

If the circumference and the area of a circle are numerically equal, then the radius of the circle is-

(a) 4 units      (b) π units      (c) 2 units      (d) 7 units

Solution :

Area of circle = πr²

Circumference of circle = 2πr

Since they are numerically equal, 

πr² = 2πr

r² = 2r

Dividing by r on both sides,

r = 2

When the circumference and area both are numerically equal, its radius will be 2 units.

Problem 2 :

The radius of a circle is 50 cm. If the radius is decreased by 50%, its area will be decreased by-

(a) 50%     (b) 75%     (c) 80%       (d) 25%

Solution :

Radius of the old circle = 50 cm (100%)

Since the radius is decreased by 50%, then radius of the new circle will be 50% of the old radius.

Area of the new circle = πr²

= π(50% of r)²

= π(0.5r)²

= π(0.25r²)

= 25% of πr²

= 25% of area of old circle.

So, 75 % of the old area is reduced.

Problem 3 :

If the sum of the areas of two circles with radii R₁ and R₂ is equal to the area of a circle of radius R, then-

a) R₁ + R₂ = R          b) R₁² + R₂2 = R²       c)  R₁ + R₂ < R

d)  R₁² + R₂2 < R²

Solution :

Area of the circle with radius R₁ = πR₁²

Area of the circle with radius R₂ = πR₂²

Sum of areas of circle with radii R₁ and R₂

πR₁² + πR₂² = πR² 

Dividing by π, we get

R₁² + R₂² = R² 

Problem 4 :

The areas of two concentric circles forming a ring are 154 square cm and 616 square cm. The breath of the ring is 

Solution :

The two circles which are having same centers is called concentric circles.

Difference between area of two concentric circles = breadth of the circle

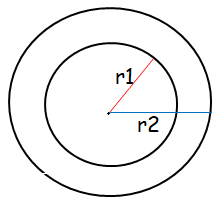
By subtracting the radius of smaller circle from the radius of larger circle is known as breadth of the ring.

Area of smaller circle = πr₁² = 154 square cm

(22/7) x r₁² = 154

r₁² = 154 x (7/22)

= 49

r₁ = 7

Area of larger circle = πr₂² = 616 square cm

(22/7) x r₂² = 616

r₂² = 616 x (7/22)

= 196

r₂ = 14

Breadth of the ring = r₂ - r₁

= 14 - 7

= 7

So, the breadth of the ring is 7 cm.

Problem 5 :

The circumference two circles are in the ratio 4:9. Find the ratio of their area. 

Solution :

Let r₁ and r₂ be the radii of the circles.

Circumference of circles are 2πr₁ and 2πr₂ 

2πr₁ : 2πr₂  =  4 : 9

r₁ : r₂  =  4 : 9

Ratio between area of circles : 

π r₁² : πr₂² = 4² : 9²

= 16 : 81

Problem 6 :

Find the area of a right- angled triangle if the radius of its circumcircle is 2.5 cm and the altitude drawn to the hypotenuse is 2 cm long

Solution :

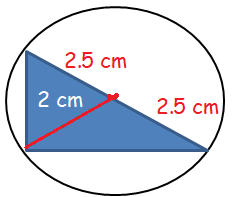
The line drawn to the hypotenuse of the right triangle is creating the angle measure 90 degree because it is altitude.

Height of the right triangle  :

Using Pythagorean theorem, 

h² = 2.5² + 2²

= 6.25 + 4

h² = 10.25

h = 3.20 cm

Base of the triangle = 3.20 cm

Area of the right triangle = (1/2) x base x height

= (1/2) x 3.20 x 3.20

= 5.12 cm²

Problem 7 :

The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 8 a.m. and 8:25 a.m.

Solution :

For every 5 minutes, angle measure created by the minute hand is 30 degree.

Angle measure created in between 12 and 5 is 150 degree

Area of the sector = (θ/360) π r²

= (150/360) π (10)²

= 130.83 cm²

Problem 8 :

The diameter of a circular pond is 17.5 cm. It is surrounded by a path of width 3.5 m. Find the area of the path.

Solution :

Diameter of the circular pond = 17.5 cm

Radius = 17.5 / 2

= 8.75 m

Width of the path = 3.5 m

Radius of large circle = 8.75 + 3.5

= 12.25 m

Area of the path = Area of the large circle - area of the small circle

= π R² - π r²

= π [(12.25)² - (8.75)²]

= π [ 150.06 - 76.56 ]

= π(73.5)

= 230.79 m²

Approximately the area of the path is 231 m²

Problem 9 :

A steel wire when bent in the form of a square encloses an area of 121 sq. cm. If the same wire is bent into the form of a circle, find the area of the circle

Solution :

Area of square = 121 sq.cm

a² = 121

a = 11

Perimeter of the square = Circumference of the circle

4a = 2 π r

4(11) = 2 π r

44/2 = π r

22 = π r

r = 22 (7/22)

r = 7

Area of the circle = π r²

= π (7)²

= 49π cm²

Problem 10 :

If the area of the circle is 154 cm², its perimeter is 

Solution :

Area of the circle = 154 cm²

π r² = 154

3.14r² = 154

r² = 154 / 3.14

r² = 49

r = 7

Perimeter of the circle = 2 π r

= 2 π (7)

= 14 π cm