PROBLEMS ON AREA OF SECTOR AND SEGMENT OF CIRCLE
Find the area of the shaded region. Leave your answer in terms of π and in simplest radical form.
Problem 1 :
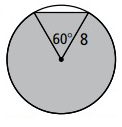
Solution:
Problem 2 :
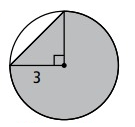
Solution:
Problem 3 :
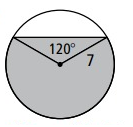
Solution:
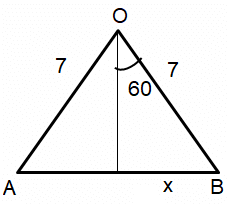
|
sin 60 = x/7 √3/2 = x/7 x = 7√3/2 AB = 7√3 |
cos 60 = h/7 1/2 = h/7 h = 7/2 |
Base of the triangle is 7√3 and height is 3.5
Area of triangle which is having central angle as 120 degree is
= (1/2) x (7√3) x 3.5
= 12.25√3 ---(2)
(1) + (2)
= 98π/3 + 12.25√3
Find the area of each shaded segment. Round your answer to the nearest tenth.
Problem 4 :
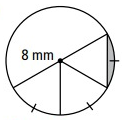
Solution:
The diameter will divide the circle into two semicircles, from the picture it is clear, we have three sectors with same measure of central angle.
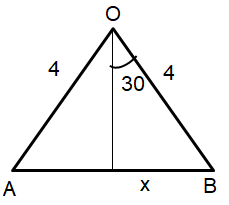
|
sin 30 = x/4 1/2 = x/4 x = 2 AB = 4 |
cos 30 = h/4 √3/2 = h/4 h = 2√3 |
Area of triangle = (1/2) x 4 x2√3
= 6.928 --(2)
Required area = 8.37 - 6.928
= 1.442
= 1.4 mm2
Problem 5 :
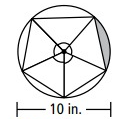
Solution:
Diameter = 10 in
radius = 10/2 = 5 in
Problem 6 :
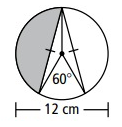
Solution:
60+150+150 ==> 360
The central angle of two equal arcs will be 150 degree.
Diameter = 12 cm
radius = 12/2 = 6 cm
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling