PROBLEMS ON AREA OF SECTOR AND LENGTH OF ARC
What is area of sector ?
A section of a circle determined by a central angle and a corresponding circular arc.
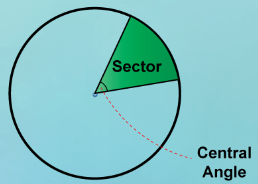
To find area of sector, we use the formula
A = (θ/360˚) ∙ πr²
What is length of arc ?
To find length of arc of a sector, we will use the formula
S = (θ/360˚) ∙ 2πr
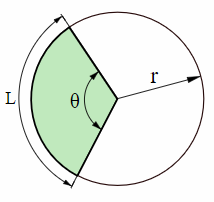
Length of arc is part of the circumference of the circle, the picture clearly shows.
Find the
length of ZY. Round to the nearest hundredth.
Problem 1 :
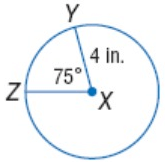
Solution :
The formula to find the arc length is
= (Arc Measure / 360˚) ∙ 2πr
Substitute r = 4 in, arc measure = 75˚ and π = 3.14
= (75˚/360˚) × 2 × 3.14 × 4
= 5.23 in
So, the length of the arc is about 5 in.
Problem 2 :
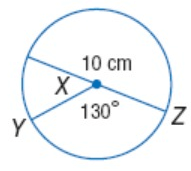
Solution :
The formula to find the arc length is
= (Arc Measure / 360˚) ∙ 2πr
Diameter = 10 cm
Substitute r = 5 cm, arc measure = 130˚ and π = 3.14
= (130˚/360˚) × 2 × 3.14 × 5
= 11.33 cm
So, the length of the arc is about 11 cm.
Problem 3 :
Find the area of a sector if the circle has a radius of 10 centimeters and the central angle measures 72.
Solution :
Given, radius = 10 cm
Central angle = 72˚
A = (θ/360˚) ∙ πr²
= (72/360) × 3.14 × (10)²
= 1/5 × 3.14 × 100
A = 62.8 cm²
So, area of sector is 62.8 cm².
Problem 4 :
Find the area of a sector if the circle has a radius of 5 inches and the central angle measures 60.
Solution :
Given, radius = 5 inches
Central angle = 60˚
A = (θ/360˚) ∙ πr²
= (60/360) × 3.14 × (5)²
= 1/6 × 3.14 × 25
A = 13.08 in²
So, area of sector is 13.08 in².
Problem 5 :
If the area of a sector is 15π square centimeters and the radius of the circle is 5 centimeters, find the measure of the central angle.
Solution :
Given, area = 15π and radius = 5 centimeters
A = (θ/360˚) ∙ πr²
15π = (θ/360˚) ∙ π ∙ (5)²
θ = 15π × 360/π × 25
θ = 216˚
So, central angle of a sector is 216˚.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling