PROBLEMS ON AREA OF CONCENTRIC CIRCLES

Problem 1 :

The areas of two concentric circles forming a ring are 154 square cm and 616 square cm. The breath of the ring is 

Solution :

The two circles which are having same centers is called concentric circles.

Difference between area of two concentric circles = breadth of the circle

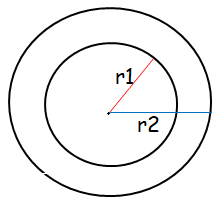
By subtracting the radius of smaller circle from the radius of larger circle is known as breadth of the ring.

Area of smaller circle = πr₁² = 154 square cm

(22/7) x r₁² = 154

r₁² = 154 x (7/22)

= 49

r₁ = 7

Area of larger circle = πr₂² = 616 square cm

(22/7) x r₂² = 616

r₂² = 616 x (7/22)

= 196

r₂ = 14

Breadth of the ring = r₂ - r₁

= 14 - 7

= 7

So, the breadth of the ring is 7 cm.

Problem 2 :

Find the area of the shaded region if radius of two concentric circles are 7 cm and 14 cm respectively and ∠𝐴𝑂𝐶 = 40 degree.

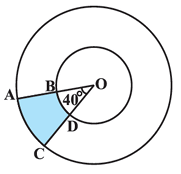
Solution :

OB is the radius of the smaller circle, OB = 7 cm

OA is the radius of the larger circle, OA = 14 cm

Area of the shaded region

= Area of the sector AOC - Area of the sector BOD

Area of sector = (θ/360) πr²

=  (θ/360) π [OA² - OB²]

= (40/360) x 3.14 x [14² - 7²]

= 1/9 x 3.14 x (196 - 49)

= 1/9 x 3.14 x  147

= 51.28 cm²

Problem 3 :

A race track is in the form of ring whose outer and inner circumferences are 506 m, 440 m respectively. Find the width of the track.

Solution :

Let r and R be the radius of smaller circle and larger circle respectively.

Circumference of large circle = 2πR

2πR = 506

2 x (22/7) x R = 506

R = 506 x (7/22) x (1/2)

R = 80.5

Circumference of small circle = 2πr

2πr = 440

2 x (22/7) x r = 440

r = 440 x (7/22) x (1/2)

r = 70

Width of the track = R - r

= 80.5 - 70

= 10.5 m

Problem 4 :

The area enclosed between the two concentric circles is 770 cm². If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.

Solution :

Let r and R be the radius and small and large circle respectively.

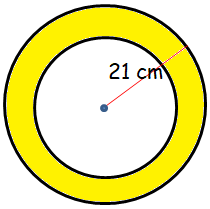
Area between the two concentric circles

= Area of larger circle - Area of smaller circle

= πR² - πr²

πR² - πr² = 770

π(R² - r²) = 770

Here R = 21

π(21² - r²) = 770

(22/7) x (441 - r²) = 770

(441 - r²) = 770 x (7/22)

441 - r² = 770 x (7/22)

441 - r² = 245

r² = 441 - 245

r² = 196

r = 14 cm

So, radius of the inner circle is 14 cm.

Problem 5 :

In the given figure, O is the center of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm, find area of the shaded region

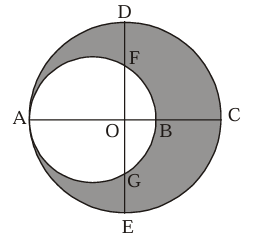
Solution :

AC = 54 cm and BC = 10 cm

Diameter of the large circle = 54 cm

Radius = 54/2 ==> 27 cm = R, BC = 10 cm

AB = AC - BC

= 54 - 10

= 44 cm

Diameter of the smaller circle = 44 cm

radius (r) = 22 cm

Area of the shaded region

= Area of the larger circle - area of the smaller circle

= π(R² - r²) 

= π(27² - 22²) 

= (22/7) x (729 - 484)

= (22/7) x 245

= 770 cm²

Problem 6 :

A race track is in the form of a ring whose inner and outer circumferences are 437 m and 503 m respectively. The width of the track is :

(a) 10.5 m    (b) 20.5 m    (c) 21 m    (d) 30 m

Solution :

Circumference of outer circle = 2πR and smaller circle = 2πr

Width = R - r

= 80.02 - 69.52

= 10.5 m

So, the required width is 10.5 m.

Problem 7 :

Diameters of three concentric circles are in the ratio 1 : 2 : 3. The sum of the circumferences of these circles is 264 cm. Find the area enclosed between second and third circles.

Solution :

Diameters of three concentric circles are x, 2x and 3x.

Radii are x/2, x and 3x/2

Sum of the circumferences of three circles = 264 cm

2πr₁ + 2πr₂ + 2πr₃ = 264

2π[x/2 + x + 3x/2] = 264

2π [(x + 2x + 3x)/2] = 264

6x = 264 x (7/22)

6x = 84

x = 84/6

x = 14

Radius of second circle = 14 cm

Radius of third circle = 3(14)/2 => 21 cm

Area between second and third circle = π(R² - r²) 

= π(21² - 14²) 

= (22/7)(441 - 196)

= (22/7) x 245

= 770 cm²