PROBLEMS ON ANGLE OF ELEVATION AND DEPRESSION

Problem 1 :

A surveyor is standing 100 meters from a bridge. She determines that the angle of elevation to the top of the bridge is 35°. If her height is 2.5 meters tall, then what is the height of the bridge?

Solution:

tan(35°) = x/100

100 tan 35° = x

100(0.7002) = x

x = 70.02 m

Since,  If her height is 2.5 meters tall creating the horizontal distance, so add the 2.5 m to the 70.02 m to determine the total height of the bridge.

70.02 m + 2.5 m = 72.52 m

The height of the bridge is 72.52 m.

Problem 2 :

From the top of a lighthouse, the angle of depression to a buoy is 25°. If the top of the lighthouse is 150 feet above sea level, find the horizontal distance from the buoy to the lighthouse.

Solution:

Problem 3 :

A jet takes off and travels 56 miles to achieve an altitude of 12.6 miles. What is the angle of elevation for the jets path?

Solution:

Problem 4 :

Avery is at the top of the Eiffel tower. When looking out she sees the Seine River at an angle of depression of 62°. The height of the tower is 324 meters. What is the horizontal distance from the Eiffel Tower to the River.

Solution:

Let x be the horizontal distance from the Eiffel Tower to the river.

So, the horizontal distance from the Eiffel Tower to the river is 172.28 m.

Problem 5 :

Find ''x''.

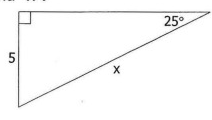
Solution:

Problem 6 :

How tall is a tree if it casts a shadow of 50 feet and they rays of the sun meet the ground at a 25° angle?

Solution:

Let x be the tall of the tree,

So, the tall of the tree is 23.32 feet.

Problem 7 :

A sonar operator on a battleship detects a submarine at a distance of 500 m (horizontally) and at an angle of depression of 37°. How deep is the submarine?

Solution:

So, submarine is 300.9 meters deep.

Problem 8 :

Find the measure of the indicated angle.

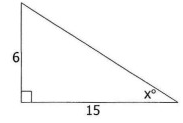
Solution:

Problem 9 :

The angle of elevation of a 110 foot crane is 45°. How high can the crane raise building material?

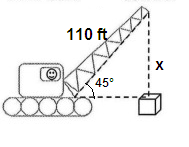
Solution:

Problem 10 :

Find ''x''.

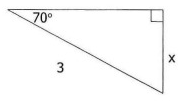
Solution:

Problem 11 :

A boy flying a kite lets out 100 feet of string making an angle of elevation of 40°. How high above the ground is the kite?

Solution:

So, the kite above the ground is 64.27 ft.

Problem 12 :

As viewed from a cliff 360 m above sea level, the angle of depression to a ship is 28°. How far is the ship from the shore?

Solution:

Problem 13 : 

The angle of elevation from a ship to the top of a lighthouse is 3°. If the ship is 1000 km from the lighthouse, how tall is the lighthouse?

Solution: