PROBLEMS ON ADJACENT ANGLES OF A PARALLELOGRAM

If ABCD is a parallelogram, we know that the opposite sides are parallel.

• Let us take AB ∥ DC in which AD and B will become the transversals.
• When two parallel lines are cut by a transversal, the co interior angles on the same side of the transversal are supplementary.

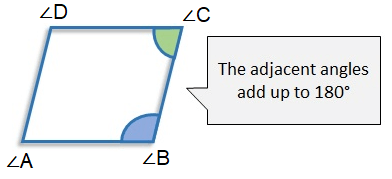
In this case,

• ∠A + ∠D = 180° and ∠B + ∠C = 180°
• ∠A + ∠B = 180° and ∠D + ∠C = 180°

Problem 1 :

If two adjacent angles of a parallelogram are (5x - 5)˚ and (10x + 35)˚, then the ratio of these angles is

a) 1: 3     b) 2: 3     c) 1: 4    d) 1: 2

Solution :

Adjacent angles add upto 180 degree.

(5x - 5)˚ + (10x + 35)˚ = 180˚

5x - 5 + 10x + 35 = 180˚

15x + 30 = 180˚

15x = 180 - 30

15x = 150

x = 10˚

(5x - 5)˚ = 5(10) - 5 = 45˚

(10x + 35)˚ = 10(10) + 35 = 135˚

Ratio = (5x - 5)˚: (10x + 35)˚

= 45: 135

= 1: 3

So, option (a) is correct.

Problem 2 :

The adjacent angles of a parallelogram are (2x - 4)˚ and (3x - 1)˚. Find the measures of all angles of the parallelogram.

Solution :

The adjacent angles of a parallelogram are supplementary.

(2x - 4)˚ + (3x - 1)˚ = 180˚

2x - 4 + 3x - 1 = 180˚

5x - 5 = 180˚

5x = 185˚

x = 185/5

x = 37˚

Thus, the adjacent angles are,

(2x - 4)˚ = 2(37) - 4 = 74 - 4 = 70˚

(3x - 1)˚ = 3(37) - 1 = 111 - 1 = 110˚

Hence, the angles are 70˚, 110˚, 70˚, 110˚.

Problem 3 :

In parallelogram ABCD, find ∠B, ∠C and ∠D.

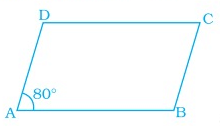
Solution :

We know that, opposite angles are equal in parallelogram.

So, ∠C = ∠A = 80˚

∠B = ∠D

∠A + ∠B = 180˚

80˚ + ∠B = 180˚

∠B = 180˚ - 80˚

∠B = 100˚

Hence, ∠B, ∠C and ∠D are 100˚, 80˚ and 100˚ respectively.

Problem 4 :

ABCD is a parallelogram. Find the value of x, y and z.

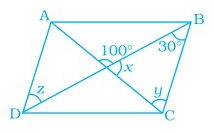
Solution :

z = 30˚ (Alternate interior angle)

100˚ + x = 180˚

x = 180˚ - 100˚

x = 80˚

In ∆OBC

80˚ + 30˚ + y = 180˚

110˚ + y = 180˚

y = 180˚ - 110˚

y = 70˚

So, x = 80˚, y = 70˚ and z = 30˚.

Problem 5 :

In parallelogram FIST, find ∠SFT, ∠OST and ∠STO.

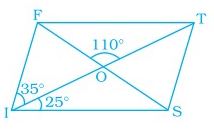
Solution :

Given, ∠FOT = 110˚, ∠OIS = 25˚ and ∠FIO = 35˚

∠OTS = ∠FIO = 35˚ (alternate interior angles are equal)

∠FOT = ∠IOS = 110˚ (vertically opposite angles are equal)

In ∆OSI,

∠OSI + ∠IOS + ∠OIS = 180˚ (sum of angles in a triangle is 180˚)

∠OSI + ∠110˚ + 25˚ = 180˚

∠OSI + 135˚ = 180˚

∠OSI = 180˚ - 135˚

∠OSI = 45˚

∠OSI = ∠SFT = 45˚ (alternate interior angles are equal)

∠FOT + ∠TOS = 180˚

110˚ + ∠TOS = 180˚

∠TOS = 180˚ - 110˚

∠TOS = 70˚

In ∆OST,

∠OTS + ∠TOS + ∠OST = 180˚

35˚ + 70˚ + ∠OST = 180˚

∠OST = 180˚ - 105˚

∠OST = 75˚

Hence, ∠OST = 75˚, ∠SFT = 45˚ and ∠OTS = 35˚

Problem 6 :

Find the values of x and y in the following parallelogram

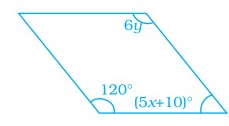
Solution :

In parallelogram opposite angles are equal.˚

6y = 120˚

y = 120/6

y = 20˚

In a parallelogram sum of corresponding angles is 180˚.

(5x + 10)˚ + 120˚ = 180˚

5x + 130˚ = 180˚

5x = 180˚ - 130˚

5x = 50˚

x = 10˚

Hence, x and y values are 10 and 20.