PROBLEMS OF ISOSCELES TRAPEZOID

Each trapezoid is isosceles. Find the measure of each angle.

Problem 1 :

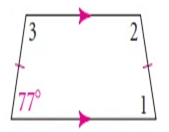
Solution :

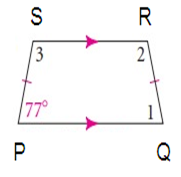
Each pair of base angles in an isosceles trapezoid must be congruent.

So, we have

m ∠P = m ∠Q = 77^º

Because ∠S and ∠P are consecutive interior angles formed by parallel lines, they are supplementary.

So, we have

m ∠P + m ∠S = 180^º

Substitute m ∠P = 77^º.

77^º + m ∠S = 180^º

Subtract 77^º from both sides.

m ∠S = 103^º

Each pair of base angles in an isosceles trapezoid must be congruent.

So, we have

m ∠S = m∠R = 103^º

Hence,

∠1 = 77^º

∠2 = 103^º

∠3 = 103^º

Problem 2 :

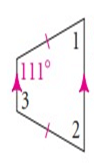
Solution :

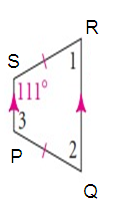
∠S + ∠R = 180

111 + ∠1 = 180

∠1 = 180 - 111

∠1 = 69

∠1 = ∠2 = 69

∠3 = 111

Problem 3 :

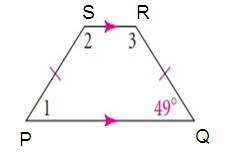
Solution :

∠1 = ∠P = ∠Q = 49

∠S + ∠P = 180

∠2 + ∠1 = 180

∠2 + 49 = 180

∠2 = 180 - 49

∠2 = 131

∠3 = 131

Problem 4 :

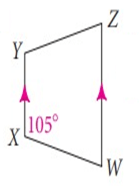
Solution :

∠X = 105, ∠Y = 105

∠W = 180 - 105

∠W = 75

∠Z = 75

Problem 5 :

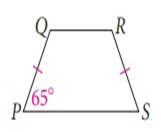
Solution :

∠P = 65, ∠S = 65

∠Q + ∠P = 180

∠Q = 180 - 65

∠Q = 115

∠R = 115

Problem 6 :

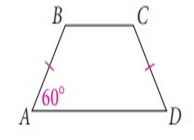
Solution :

∠A = 60, ∠D = 60

∠B + ∠A = 180

∠B = 180 - 60

∠B = 120

∠C = 120