PROBLEMS INVOLVING QUADRATIC FUNCTIONS

The equation which is in the form

f(x) = ax² + bx + c

is known as quadratic equation.

The graphical form of quadratic function is parabola. Based on the signs of a, we can say the parabola opens upward or downward.

• If sign of a is +, then the parabola opens upward.
• If sign of a is -, then the parabola opens downward.

Equation of parabola can be converted into three different forms.

• Standard form
• Vertex form
• Factored form.

Problem 1 :

Which of the following gives the solution set for the polynomial equation below?

x²−11𝑥+19 = −5

A. {-3, -8}     B. {3, 8}       C. {-3, 8}      D. {3, -8}

Solution :

x²−11𝑥+19 = −5

Add 5 on both sides.

x²−11𝑥+19+5 = 0

x²−11𝑥+24 = 0

(x - 3) (x - 8) = 0

Equating each factors to zero, we get

x = 3 and x = 8

So, the solution set is {-8, 3}

Problem 2 :

Which of the following could be the equation for the polynomial function below?

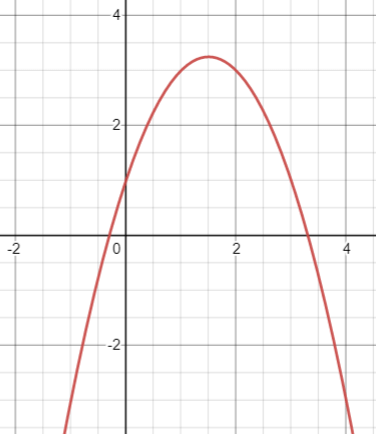
A. y = −x²+3x+1     B. y = x²−0.25x+3.25

C. y = x²−x+3       D. y=−x²+0.25x−3.25

Solution :

From the graph, the parabola opens down. So, we can clearly reject options B and C.

Option (A) :

𝑦 = −x²+3x+1

Converting into vertex form, we get

h = 3/2 and k = 13/4

From the graph, the vertex in between 2 and 4. So, option A is correct.

Problem 3 :

Which of the following is an equation for the function below and gives the coordinates of the vertex as constants or coefficients?

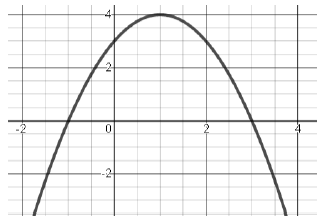
A. y = −(x−3)(x+1)         B. y = −x²+2x+3

C. y = (x+1)²+4             D. y = −(x−1)²+4

Solution :

y = −(x−3)(x+1)

Equating each factor to zero, we get

x = 3 and x = -1

By observing the graph given above, it opens downward and x-intercepts are 3 and -1.

Finding vertex :

y = −(x−3)(x+1)

y = −(x²-3x+1x−3)

y = −(x²-2x−3)

y = −(x² - 2⋅x⋅1 + 1² -1² − 3)

y = −[(x-1)² - 4]

y = −(x-1)² + 4

Vertex is (1, 4).

So, option A is correct.

Problem 4 :

How many solutions are there to the following system of equations?

y = −(1/2)x²+7 and 𝑦 = −2x²+5

A. 0        B. 1       C. 2         D. 3

Solution :

y = −(1/2)x²+7 ------(1) y = −2x²+5  ------(2)

To find the points of intersection, we can solve (1) and (2).

(1) = (2)

−(1/2)x²+7 = −2x²+5 

-x² + 14 = -4x² + 10

3x² = -10 - 14

3x² = -24

x² = -8

x = √-8

It is not real number, so it will not have solution. So, zero solution is the answer.