PROBLEM SOLVING ON QUADRATIC EQUATION FOR SAT

Problem 1 :

In the xy-plane, what is the distance between the two x-intercepts of the parabola

y = x² - 3x - 10 ?

a)  3      b)  5      c)  7    d)  10

Solution :

y = x² - 3x - 10

To find x-intercepts, we equation y to 0.

x² - 3x - 10 = 0

(x - 5) (x + 2) = 0

x = 5 and x = -2

Distance between x-intercepts = 5 + |-2|

= 5 + 2

 = 7

Problem 2 :

What are the solutions to x² + 4x + 2 = 0 ?

a) -2 ± √2     b) 2 ± 2√2      c) -2 ± 2√2   d) -4 ± 2√2

Solution :

Problem 3 :

If a < 1 and 2a² - 7a + 3 = 0, what is the value of a ?

Solution :

2a² - 7a + 3 = 0

2a² - 6a - a + 3 = 0

2a(a - 3) -1(a - 3) = 0

(2a - 1)(a - 3) = 0

2a = 1, a = 1/2

a = 3

So, the value of a is 3.

Problem 4 :

3x² + 10x = 8

If a and b are two solutions to the equation above and a > b, what is the value of b² ?

a)  4/9    b)  2/3    c) 4    d)  16

Solution :

3x² + 10x = 8

3x² + 10x - 8 = 0

3x² + 12x - 2x - 8 = 0

3x(x + 4) - 2(x + 4) = 0

(3x - 2) (x + 4) = 0

x = 2/3 and x = -4

Since a > b, then a = 2/3 and b = -4

b² = (-4)² = 16

Problem 5 :

What is the sum of the solutions of (2x- 3)² = 4x + 5 ?

Solution :

(2x- 3)² = 4x + 5

Using the algebraic identity, (a - b)²

(2x)²  -2(2x) (3) + 3² = 4x + 5

4x² - 12x + 9 - 4x - 5 = 0 

4x² - 16x + 4 = 0

x² - 4x + 1 = 0

Sum of solutions (α+β) = -b/a

(α+β) = -(-4) / 1

(α+β) = 4

Problem 6 :

y = -3

y = x² + cx

In the system of equations, c is a constant. For which of the following values of c does  the system of equations have exactly two real solutions ?

a)  -4    b)  1    c) 2    d)  3

Solution :

y = -3   ----(1)

y = x² + cx  ----(2)

(1) = (2)

-3 = x² + cx

x² + cx + 3 = 0

So, option a is correct.

Problem 7 :

At which of the following points does the line with equation y = 4 intersect the parabola y = (x + 2)² - 5 in the xy-plane ?

a)  (-1, 4) and (-5, 4)      b)  (1, 4) and (-5, 4)

c)  (1, 4) and (5, 4)        d)  (-11, 4) and (7, 4)

Solution :

y = 4 ------(1)

y = (x + 2)² - 5 ------(2)

(1) = (2)

(x + 2)² - 5 = 4

(x + 2)² = 9

x + 2 = ±3

x+2 = 3 and x + 2 = -3

x = 3 - 2 and x = -3 - 2

x = 1 and x = -5

So, points of intersections are (1, 4) and (-5, 4).

Problem 8 :

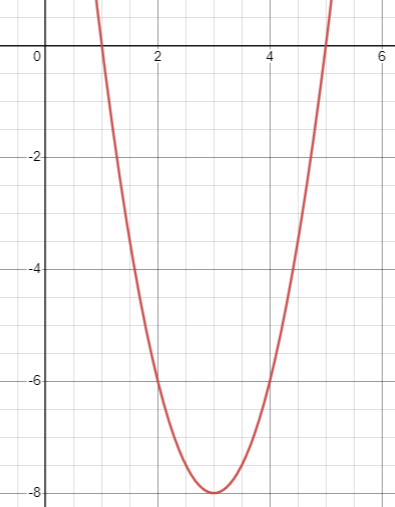
Which of the following equations represents the parabola shown in the xy-plane above ?

a)  y = (x - 3)² - 8           b)  y = (x + 3)² + 8

c)  y = 2(x - 3)² - 8         d)  y = 2(x + 3)² - 8

Solution :

By observing the given parabola, we get 

x-intercepts are 1 and 5. vertex is at (3, -8)

y = a(x - h)² + k

y = a(x - 3)² - 8

Applying (1, 0), we get

0 = a(1 - 3)² - 8

8 = a(-2)²

4a = 8

a = 2

y = 2(x - 3)² - 8

Problem 9 :

For what value of t does the equation v = 5t - t² result in the maximum value of v ?

Solution :

v = 5t - t²

v = - t² + 5t

Minimum value is at 5/2.

Problem 10 :

P = m² - 100m - 120000

The monthly profit of a mattress company cab be modeled by the equation above, where P is the profit in dollars, and m is the number of mattresses the company must sell in the given month so that it does not lose money during that month ?

Solution :

P = m² - 100m - 120000

P = m² - 2(m) 50 + 50² - 50² - 120000

P = (m - 50)² - 2500 - 120000

P = (m - 50)² - 122500

The minimum number of mattresses sold is 50.

Problem 11 :

y = -3

y = ax² + 4x - 4

In the system if equations above, a is a constant. For which of the following of a does the system of equations have exactly one real solution ?

a)  -4        b)  -2        c)  2       d) 4

Solution :

y = -3 ---(1)

y = ax² + 4x - 4 -----(2)

(1) = (2)

-3 = ax² + 4x - 4

ax² + 4x - 4 + 3 = 0

ax² + 4x - 1 = 0

When a = -4

-4x² + 4x - 1 = 0

Finding nature of roots,

= b² - 4ac

a = -4, b = 4 and c = -1

= 4² - 4(-4)(-1)

= 16 - 16

= 0

Since the value of b² - 4ac is 0, it will have two real roots. So, a = -4.

Problem 12 :

f(x) = -x² + 6x + 20

The function f is defined above, which of the following is equivalent form of f(x) displays the maximum value of f as a constant or coefficient ?

a)  f(x) = -(x - 3)² + 11          b)  f(x) = -(x - 3)² + 29  

c)  f(x) = -(x + 3)² + 11        d)  f(x) = -(x + 3)² + 29

Solution :

f(x) = -x² + 6x + 20

f(x) = -[x² - 6x - 20]

f(x) = -[x² - 2x(3) + 3² - 3² - 20]

f(x) = -[(x - 3)² - 9 - 20]

f(x) = -[(x - 3)² - 29]

f(x) = -(x - 3)² + 29

So, option b is correct.

Problem 13 :

y = a(x - 3)(x - k)

In the quadratic equation above a and k are constants. If the graph of the equation in the xy-plane is a parabola with vertex (5, -32). What is the value of a ?

a)  2     b)  5       c)  6      d) 8

Solution :

y = a(x - 3)(x - k)

By observing the vertex form, we see one of the x-intercept is 3. The vertex will lie in between the x-intercepts and it is one of the points on the parabola.

Distance between 3 and 5 is 2. Moving forward 2 units from 5, we get 7. So, the another x-intercept is 7. k = 7.

-32 = a(5 - 3)(5 - 7)

-32 = 2a(- 2)

4a = 32

a = 32/4

a = 8

Problem 14 :

In the xy-plane, he line y = 2x + b intersects the parabola y = x² + bx + 5 at the point (3, k). If b is a constant, what is the value of k ?

Solution :

y = 2x + b -----(1)

y = x² + bx + 5 ------(2)

(1) = (2)

2x + b = x² + bx + 5

x² + bx + 5 - 2x - b = 0

x² + (b - 2)x + 5 - b = 0

Point of intersection is (3, k).

When x = 3

3² + (b - 2)3 + 5 - b = 0

9 + 3b - 6 + 5 - b = 0

3 + 3b + 5 - b = 0

2b + 8 = 0

b = -4

(3, k) will appear in both line and parabola.

k = 2(3) + b

k = 6 - 4

k = 2

So, the value of k is 2.