PROBLEM SOLVING ON ANGLES PRACTICE FOR DIGITAL SAT

Problem 1 :

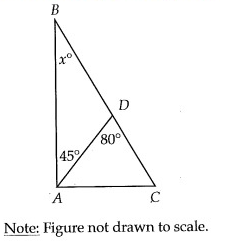
In the figure above, what is the value of x?

Solution:

From the figure,

∠BDA + ∠ADC = 180°

x + 80 = 180°

x = 180 - 80°

x = 100°

Problem 2 :

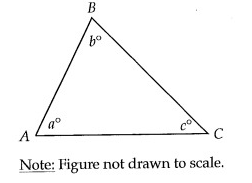
In the figure above, AB = AC and c = 50°. What is the value of a?

A) 65       B) 70     C) 75     D) 80

Solution:

∠ABC = ∠ACB

If two sides of a triangle are congruent, then the angles opposite those sides are congruent.

b = c

∠ABC = c

b = 50°

∠ABC + ∠ACB + ∠BAC = 180°

b + c + a = 180°

50° + 50° + a = 180°

100 + a = 180

a = 80°

So, option (D) is correct.

Problem 3 :

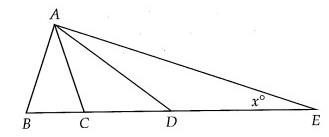
In the figure above, ∠BAC = 20° and AB = AC. If triangles ACD and ADE are isosceles, what is the value of x?

A) 10       B) 15         C) 20             D) 25

Solution:

∠BAC = 20°

Since AB and AC are equal, it will make equal angles only.

∠ABC = ∠ACB

2∠ABC + 20 = 180

2∠ABC = 160

∠ABC = 160/2 ==> 80

∠ACD = 180 - 80 ==> 100

In triangle ACD, the other two angles must be acute angle.

∠CDA = ∠CAD (isosceles triangle)

∠CDA = ∠CAD = 40

∠ADE = 140

Since ADE is isosceles triangle and already we have obtuse angle, the other two must be equal and acute angles.

x = 20

∠DAE = 20

Problem 4 :

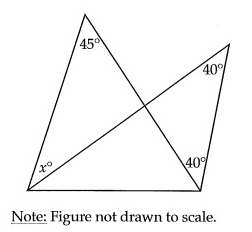
In the figure above, what is the value of x?

Solution:

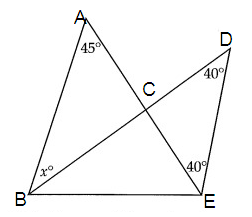
In triangle DCE,

40 + 40 + x = 180°

80 + x = 180

x = 100°

In triangle ACB,

100 + 45 + x = 180°

145 + x = 180°

x = 180 - 145

x = 35

Problem 5 :

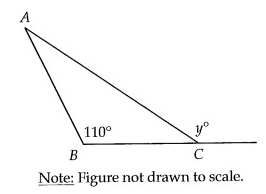
In the figure above, AB = BC and ∠ABC = 110°. What is the value of y?

A) 125         B) 130         C) 135              D) 145

Solution:

If two sides of a triangle are congruent, then the angles opposite those sides are congruent.

∠BAC = ∠ACB

∠ABC + ∠ACB + ∠BAC = 180°

∠ABC + ∠ACB + ∠ACB = 180°

110 + ∠ACB + ∠ACB = 180°

 ∠ACB = 35°

∠ACB + ∠ACD = 180°

35° + y= 180°

y = 145°

So, option (D) is correct.

Problem 6 :

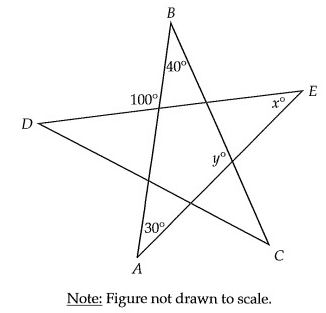
In the figure above, AB, BC, CD, DE and EA are line segments. What is the value of x + y?

Solution:

In triangle BAY,

40° + y + 30° = 180°

70 + y = 180°

y = 110°

30 + 100 + x = 180

x = 180 - 130

x = 50

x + y = 50 + 110

= 160

Problem 7 :

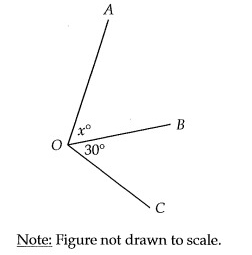
In the figure above, the measure of ∠AOB is 2/5 the measure of ∠AOC. What is the value of x?

Solution:

∠AOB = 2/5∠AOC

∠BOC = 30°

∠AOC = x + 30°

∠AOB = x

x = 2/5(x + 30°)

5x = 2(x + 30)

5x = 2x + 60

5x - 2x = 60

3x = 60

x = 60/3

x = 20

So, the value of x is 20.

Problem 8 :

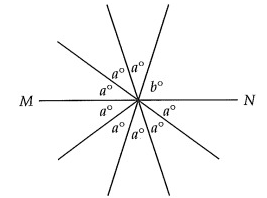
In the figure above, MN is a line. What is the value of b?

Solution:

3a° + b° = 180°

5a = 180°

a = 36

3(36) + b = 180°

108 + b = 180°

b = 72°

Problem 9 :

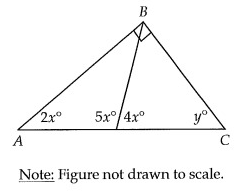
In right triangle ABC above, what is the value of y?

Solution:

5x° + 4x° = 180°

9x° = 180°

x = 20°

2x° + y° = 90°

2(20) + y° = 90°

y = 90° - 40°

y = 50°

Problem 10 :

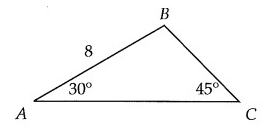
In the figure above, ∠BAC = 30°, ∠BCA = 45°, and AB = 8. What is the length of BC?

A) 4        B) 4√2     C) 4√3     D) 8√2

Solution:

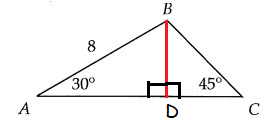
By drawing a perpendicular bisector, the side which is opposite to 90 degree is hypotenuse. BD is the smaller side

2 smaller side = 8

BD = 4

BC² = BD² + DC²

BC² = 4² + 4²

BC² = 16 + 16

BC² = 32

BC = √32

BC = 4√2

So, option B is correct.

Problem 11 :

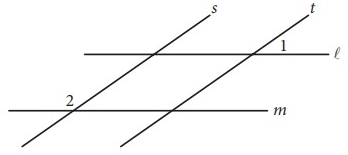
In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35°, what is the measure of ∠2?

A) 35°         B) 55°       C) 70°          D) 145°

Solution:

Corresponding angles are equal.

∠1 = 35°

∠2 + ∠1 = 180°

∠2 + 35 = 180°

∠2 = 145°

So, option (D) is correct.

Problem 12 :

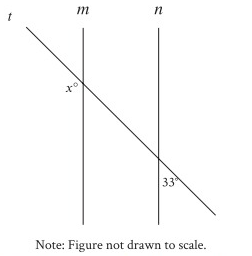
In the figure, line m is parallel to line n, and line t intersects both lines. What is the value of x?

A) 33     B) 57    C) 123    D) 147

Solution:

Corresponding angles are equal.

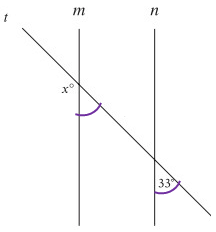
x = 180 - 33

x = 147

So, option (D) is correct.

Problem 13 :

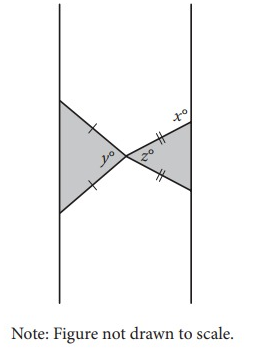
Two isosceles triangles are shown above. If 180 - z = 2y and y = 75, what is the value of x?

Solution:

180 - z = 2y

180 - z = 2(75)

180 - z = 150

z = 30

In an isosceles triangle, the base angles are equal. So,

x = z

x = 30