PROBLEM SOLVING IN CIRCLE CONIC SECTIONS

Problem 1 :

The center of the circle inscribed in a square formed by the lines x² - 8x + 12 = 0 and y² - 14y + 45 = 0 is

a)  (4, 7)      b) (7, 4)      c)  (9, 4)     d)  (4, 9)

Solution :

x² - 8x + 12 = 0 and y² - 14y + 45 = 0

Solving equations, we get

(x - 6)(x - 2) = 0 and (y - 9)(y - 5) = 0

x = 6, x = 2 and y = 9, y = 5

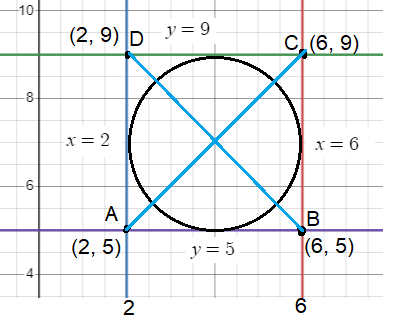
By plotting the points and figuring out the midpoint of AC, we will get center of the circle.

Midpoint of AC = (2 + 6)/2, (5 + 9)/2

= 8/2, 14/2

= (4, 7)

So, center of the circle is (4, 7).

Problem 2 :

The equation of the normal to the circle x² + y² - 2x - 2y + 1 = 0 which is parallel to the line 2x + 4y = 3 is

a)  x + 2y = 3     b)  x + 2y + 3 = 0

c)  2x + 4y + 3 = 0        d)  x - 2y + 3 = 0

Solution :

x² + y² - 2x - 2y + 1 = 0

2g = -2, g = -1

2f = -2, f = -1

Center (-g, -f) ==> (1, 1) and radius = √g² + f² - c 

radius = √1² + 1² - 1 ==> 1

The normal is parallel to the given line and it will pass through the center of the circle.

2x + 4y = 3

Slope of the normal drawn to the circle :

m = -1/2

will pass through the point (1, 1)

y - y₁= m(x - x₁)

y - 1= (-1/2)(x - 1)

2y - 2 = -1(x - 1)

2y - 2 = -x + 1

x + 2y - 2 - 1 = 0

x + 2y - 3 = 0

x + 2y = 3

Problem 3 :

The radius of the circle is passing through the point (6, 2) two of whose diameters are x + y = 6 and x + 2y = 4 is

a)  10        b) 2√5      c) 6        d)  4

Solution :

Diameters will intersect each other at center.

x + y = 6 ------(1)

x + 2y = 4 ------(2)

(1) - (2)

y - 2y = 6 - 4

-y = 2

y = -2

Applying the value of y in (1)

x - 2 = 6

x = 8

Center of the circle is (8, -2)

Equation of the circle :

(x - h)² + (y - k)² = r²

(x - 8)² + (y + 2)² = r²

It passes through the point (6, 2).

(6 - 8)² + (2 + 2)² = r²

(-2)² + 4² = r²

r² = 4 + 16

r² = 20

r = √20

r = 2√5

Problem 4 :

The equation of the circle passing through the foci of the ellipse 

having center at (0, 3) is 

a) x² + y² - 6y - 7 = 0         b) x² + y² - 6y + 7 = 0

c) x² + y² - 6y - 5 = 0          d) x² + y² - 6y + 5 = 0

Solution :

From the given equation of ellipse, we know that it must be symmetric about x-axis.

Distance between center and foci of the ellipse. Center of the circle and foci of the ellipse lie on the same horizontal line. 

Equation of the circle :

(x - h)² + (y - k)² = r²

(x - 0)² + (y - 3)² = 4²

x² + y² -6y + 9 = 16

x² + y² - 6y + 9 - 16 = 0

x² + y² - 6y - 7 = 0

Problem 5 :

Let C be the circle with center at (1, 1) and radius = 1. If T is the circle centered at (0, y) passing through the origin and touching the circle C externally, then the radius of T is equal to

a)  √3/√2      b)  √3/2      c)  1/2     d)  1/4

Solution :

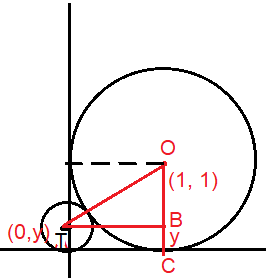
In triangle TOB, OB = 1 - y, TB = 1, TO = y + 1

So, the radius of the circle T is 1/4. 

Problem 6 :

If the coordinates at one end of a diameter of the circle 

x² + y² - 8x - 4y + c = 0

are (11, 2) the coordinates of the other end are 

a)  (-5, 2)    b)  (-3, 2)    c) (5, -2)     d) (-2, 5)

Solution :

x² + y² - 8x - 4y + c = 0

Finding center of the circle :

2g = -8, g = -4

2f = -4, f = -2

(-g, -f) ==> (4, 2)

Distance between center and one end of the diameter = distance between center and other end of the diameter

(or)

Midpoint of the endpoints of the diameter = center

Let (a, b) be the other endpoint of the diameter.

(11 + a)/2, (2 + b)/2 = (4, 2)

So, the other endpoint is (-3, 2).

Problem 6 :

The circle passing through (1, -2) and touching the axis of x at (3, 0) passing through the point

a)  (-5, 2)     b) (2, -5)      c) (5, -2)   d) (-2, 5)

Solution :

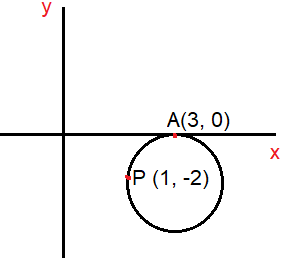
Center will be in the form of (3, -k)

(x - h)² + (y - k)² = r²

(x - 3)² + (y + k)² = r²  ---(1)

The circle is passing through the points (1, -2) and (3, 0)

Applying the point (3, 0), we get

(3 - 3)² + (0 - k)² = r²

(0 - k)² = r²

k² = r²

k = r

Applying the point (1, -2), we get

(1 - 3)² + (-2 - r)² = r²

4 + 4 + 4r + r² = r²

4r = -8

r = -2 then k = -2

Center (3, -k) ==>(3, 2)

Applying the value of r in (1), we get

(x - 3)² + (y - k)² = (-2)² 

(x - 3)² + (y + 2)² = 4

Option c :

(5, -2)

(5 - 3)² + (-2 + 2)² = 4

Satisfies. So, option c is correct.