PRECALCULUS PRACTICE PROBLEMS

Problem 1 :

Find the product and write the result in standard form.

(8 – 3i) (-2 – 3i)

Solution :

(8 – 3i) (-2 – 3i)

= -16 - 24i + 6i + 9i²

= -16 - 18i - 9

= -25 - 18i

Problem 2 :

Divide and express the result in standard form.

Solution :

Problem 3 :

Solve the quadratic equation using the quadratic formula. Express the solution in standard form.

4x² – 3x + 1 = 0

Solution :

4x² – 3x + 1 = 0

a = 4, b = -3, and c = 1

Problem 4 :

Find the coordinates of the vertex for the parabola defined by the given quadratic function.

f(x) = 5x² + 10x - 5

Solution :

Given the quadratic function f(x) = 5x² + 10x - 5

a = 5, b = 10, c = -5

x = -b/2a

= -10/2(5)

= -10/10

x = -1

When x = -1 substitute the given function .

f(x) = 5(-1)² + 10(-1) - 5

= 5 - 10 - 5

f(x) = -10 

So, the vertex for the parabola is (-1, -10).

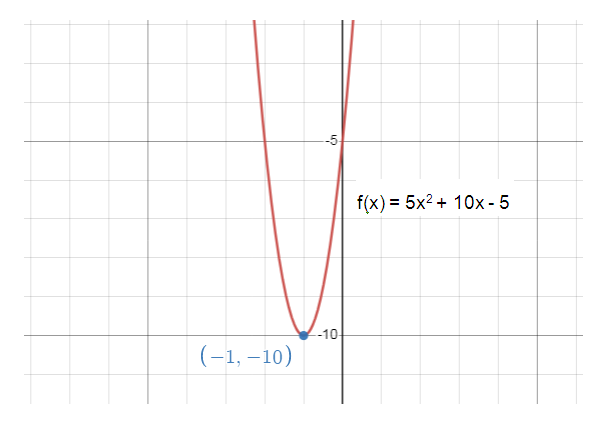
Problem 5 :

Solve the problem.

The cost in millions of dollars for a company to manufacture x thousand automobiles is given by the function

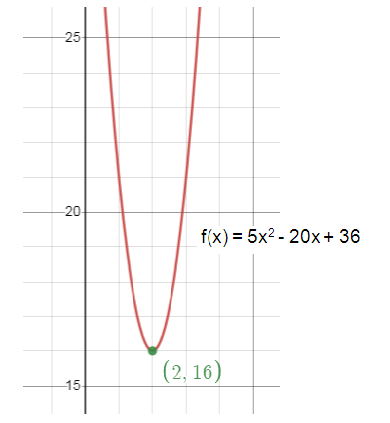
C(x) = 5x² – 20x + 36

Find the number of automobiles that must be produced to minimize the cost.

Solution :

Given the function C(x) = 5x² – 20x + 36

= 5x² – 20x + 20 + 16

= (5x² – 20x + 20) + 16

= 5(x² - 4x + 4) + 16

= 5(x - 2)² + 16

vertex = (2, 16)

x = 2 minimize the cost function.

A company to manufacture the automobiles = x thousand automobiles

= 2(1000)

= 2000

So, the required the number of automobiles is 2000.

Problem 6 :

Find the zeros of the polynomial function.

f(x) = x³ + 4x² – 4x - 16

Solution :

f(x) = x³ + 4x² – 4x - 16

 = x²(x + 4) – 4(x + 4)

= (x² - 4) (x + 4)

= (x² - 2²) (x + 4)

= (x + 2) (x - 2) (x + 4)

Zeroes are 

x = -2, x = 2 and x = -4

Problem 7 :

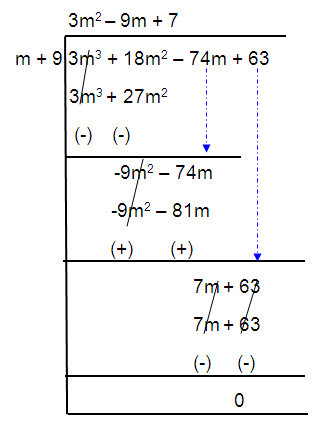
Divide using long division or synthetic division

Solution :

Long  division :

Synthetic division :

m + 9 = 0

m = -9

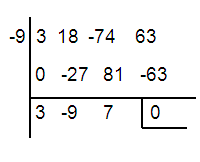
3m² - 9m + 7 = 0

Problem 8 :

Find a rational zero of the polynomial function and use it to find all the zeros of the function.

f(x) = x³ – 8x² + 19x - 14

Solution :

Given, f(x) = x³ – 8x² + 19x - 14

 (x - 2)(x² - 6x + 7) = 0

x - 2 = 0 and x² - 6x + 7 = 0

x = 2 

x² - 6x + 7 = 0

a = 1, b = -6, c = 7

x = 2, x = 3 + √2 and x = 3 - √2

Problem 9 :

Find the domain of the rational function.

Solution :

x² - 49x ≠ 0

x(x - 49) ≠ 0 

x ≠ 0  and x - 49 ≠  0 

x ≠ 0 and x ≠ 49

So, domain 

(-∞, 0) ∪ (0, 49) ∪ (49, ∞)

Problem 10 :

Find the vertical asymptotes, if any, of the graph of the rational function.

Solution :

To find the vertical asymptotes, set the denominator equal to zero and solve for x.

x - 6 = 0 and x - 9 = 0

So, vertical asymptotes are x = 6, x = 9