PRACTICE SPECIAL RIGHT TRIANGLES FOR HONORS GEOMETRY

Problem 1 :

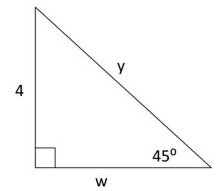
Solution :

Finding the value of y :

By 45^º - 45^º - 90^º triangle theorem,

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = y, and shorter length = 4.

y = 2 ⋅ 4

y = 8

So, the value of y is 8.

Finding the value of w :

By 45^º - 45^º - 90^º triangle theorem,

longer length = √3 ⋅ shorter length

Here, longer length = w, and shorter length = 4.

w = √3 ⋅ 4

w = 4√3

So, the value of w is 4√3.

Problem 2 :

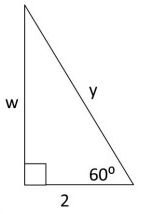
Solution :

Finding the value of y :

By 60^º - 30^º - 90^º triangle theorem,

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = y, and shorter length = 2.

y = 2 ⋅ 2

y = 4

So, the value of y is 4.

Finding the value of w :

By 60^º - 30^º - 90^º triangle theorem,

longer length = √3 ⋅ shorter length

Here, longer length = w, and shorter length = 2.

w = √3 ⋅ 2

w = 2√3

So, the value of w is 2√3.

Problem 3 :

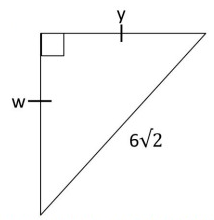
Solution :

Finding the value of y :

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = 6√2, and shorter length = y.

6√2 = 2 ⋅ y

6√2/2 = y

3√2 = y

So, the value of y is 3√2.

Finding the value of w :

longer length = √3 ⋅ shorter length

Here, longer length = w, and shorter length = y.

w = √3 ⋅ 3√2

w = 3√6

So, the value of w is 3√6.

Problem 4 :

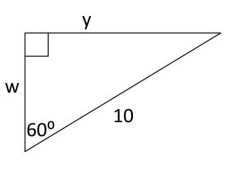
Solution :

Finding the value of w :

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = 10, and shorter length = w.

10 = 2 ⋅ w

10/2 = w

5 = w

So, the value of w is 5.

Finding the value of y :

longer length = √3 ⋅ shorter length

Here, longer length = y, and shorter length = w.

y = √3 ⋅ 5

y = 5√3

So, the value of y is 5√3.

Problem 5 :

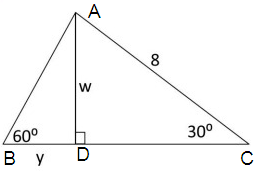
Solution :

Finding the value of w :

∠ADC is a 30^º - 60^º - 90^º triangle.

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = 8, and shorter length = w.

8 = 2 ⋅ w

8/2 = w

4 = w

So, the value of w is 4.

Finding the value of y :

∠ABD is a 30^º - 60^º - 90^º triangle.

longer length = √3 ⋅ shorter length

Here, longer length = y, and shorter length = w.

y = √3 ⋅ 4

y = 4√3

So, the value of y is 4√3.

Problem 6 :

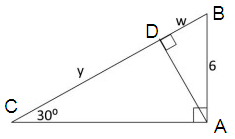
Solution :

Finding the value of w :

∠ADB is a 30^º - 60^º - 90^º triangle.

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = 6, and shorter length = w.

6 = 2 ⋅ w

6/2 = w

3 = w

So, the value of w is 3.

Finding the value of y :

∠ADC is a 30^º - 60^º - 90º triangle.

longer length = √3 ⋅ shorter length

Here, longer length = y, and shorter length = w.

y = √3 ⋅ 3

y = 3√3

So, the value of y is 3√3.

Problem 7 :

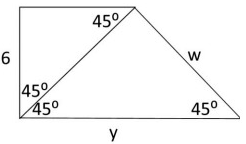
Solution :

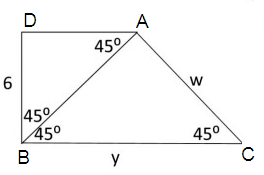
Given triangle is a 45^º - 45^º - 90^º triangle.

Finding the value of w :

So, the value of w is 6√2. 

Finding the value of y :

∠ADC is a 30^º - 60^º - 90^º triangle. 

So, the value of y is 12.

Problem 8 :

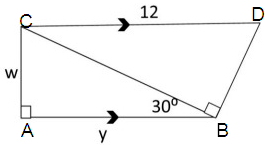
Solution :

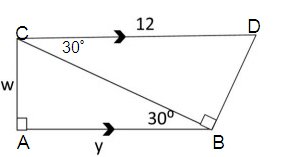
AB and CD are parallel.

Then ∠DCB is a 30^º (alternate triangle). 

∠CDB = 60^º

hypotenuse =  2 ⋅  shorter length

12 = 2 ⋅ shorter length

12/2 =  shorter length

6 =  shorter length

Finding the value of y :

∠CDB is a 30^º - 60^º - 90^º triangle.

Here, hypotenuse = 12, and shorter length = 6.

y = 2 ⋅ 6

y = 12

So, the value of y is 12.

Finding the value of w :

∠BCA is a 30^º - 60^º - 90^º triangle.

longer length = √3 ⋅ shorter length

Here, longer length = y, and shorter length = w.

y = √3 ⋅ w

12 = √3 ⋅ w

12/√3 = w

Problem 9 :

The shortest side of a 30^º - 60^º - 90^º triangle is 15. Find the length of the other sides.

Solution :

Let x be the shortest side.

x = 15

hypotenuse =  2 ⋅  shorter length

hypotenuse = 2 ⋅ 15

hypotenuse = 30

To find the length of the other sides :

longer length = √3 ⋅ shorter length

Here, longer length = y, and shorter length = 15.

y = √3 ⋅ 15

y = 15√3

Problem 10 :

The hypotenuse of a 30º - 60º - 90º triangle is 18. Find the length of the other sides.

Solution :

hypotenuse = 18

hypotenuse =  2 ⋅  shorter length

18 = 2 ⋅ shorter length

18/2 = shorter length

shorter length = 9

To find the length of the other sides :

longer length = √3 ⋅ shorter length

Here, longer length = y, and shorter length = 9.

y = √3 ⋅ 9

y = 9√3

Problem 11 :

One leg of a 45º - 45º - 90º triangle is 9. Find the length of the other sides.

Solution :

Let hypotenuse be given side.

By using Pythogorean theorem

a² + b² = c²

a² + b² = 9²

Let a² = b²

a² + a² = 9²

2a² = 9²

2a² = 81

a² = 81/2

a =√(81/2)

a = 9/√2

a = 9√2/2

b = 9√2/2