PRACTICE QUESTIONS ON GEOMETRY FOR PSAT

Problem 1 :

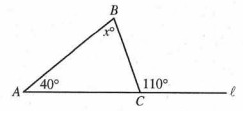
In the figure above, points A and C lie on line l. What is the value of x ?

A) 30        B) 40          C) 50        D) 60         E) 70

Solution:

∠ABC + ∠BAC = ∠BCE

x + 40° + 110°

x = 110 - 40

x = 70°

Problem 2 :

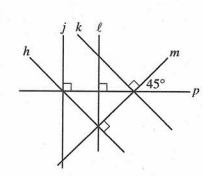
How many pairs of parallel lines are in the figure above?

A) One     B) Two      C) Three         D) Four       E) Five

Solution:

Line j and l

Line h and k

Therefore 2 pair of parallel lines.

So, option (B) is correct.

Problem 3 :

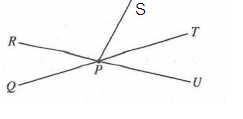
In the figure above, point P lies on line segments QT and RU. If the measure of ∠RPQ is 40° and the measure of ∠SPU is 70°, what is the measure of ∠SPT?

A) 30°         B) 35°       C) 40°       D) 45°          E) 50°

Solution:

∠RPQ = ∠TPU (vertically opposite angles)

∠RPQ = 40°

So, ∠TPU = 40°

∠SPT = ∠SPU - ∠TPU

= 70° - 40°

∠SPT = 30°

So, option (A) is correct.

Problem 4 :

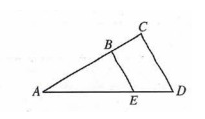
In △ACD above, BE||CD nd the length of AB is 2/3 the length of AC, if the length of AD is 12, what is the length of AE?

Solution:

Let AE be x cm.

ED = 12 - x cm

Problem 5 :

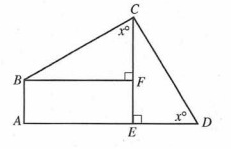
In the figure above, △BCF and △CDE have the same size and same shape. If ABFE is a rectangle, AB = 2, and DE = 3, what is the area of ABCD?

A) 15        B) 20        C) 25         D) 30         E) 40

Solution:

In triangle BCF and DEC, since these two triangles are congruent,

BC = CD

BF = CE

CF = ED

CE = CF + FE

CE = 5

Height of the triangle = 5, base = 3

Required area = 2(area of triangle) + area of rectangle

= 2(1/2 x 5 x 3) + 2 x 5

= 15 + 10

= 25

Problem 6 :

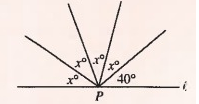
In the figure above, point P is on line l. What is the value of x?

A) 25           B) 30            C) 35           D) 40      E) 45

Solution:

x + x + x + x + 40° = 180°

4x + 40° = 180°

4x = 180 - 40

4x = 140

x = 140/4

x = 35 

So, option (C) is correct.

Problem 7 :

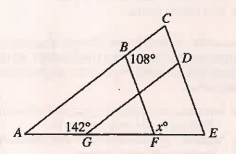
In the figure above, AC||GD and CE||BF. What is the value of x?

Solution:

∠BAF + ∠AGD = 180°

∠BAF + 142 = 180°

∠BAF =38°

∠ABH + ∠CBH = 180°

∠ABH + 108 = 180°

∠ABH = 72°

∠ABF = ∠ABH

∠ABF = 72°

∠ABF + ∠BAF = ∠BFE

72 + 38 = x

x = 110°

Problem 8 :

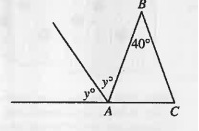
In △ABC above, AB = BC. What is the value of y?

A) 40      B) 55      C) 65       D) 70        E) 90

Solution:

x + x + 40 = 180°

2x + 40 = 180°

2x = 180 - 40

2x = 140

x = 70°

x + y + y = 180°

70 + 2y = 180

2y = 180 - 70

2y = 110

y = 55°

So, option (B) is correct.

Problem 9 :

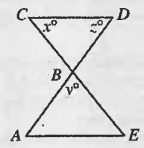
In the figure above, AE||CD and AB and BE have equal length. If y = 81, what is the value of x?

Solution:

Given, y = 81

x + y + z = 180°

x + 81 + x = 180°

2x + 81 = 180°

2x = 180 - 81

2x = 99

x = 99/2

x = 49.5

Problem 10 :

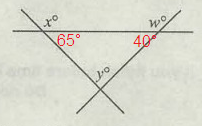
Three lines intersect in the figure above. If x = 115 and w = 140, what is the value of y?

A) 55        B) 65       C) 75      D) 95        E) 105

Solution:

Interior angle = 180° - 115°

= 65°

Interior angle = 180° - 140°

= 40°

65 + 40 + y = 180°

105 + y = 180

y = 180 - 105

y = 75°

So, option (C) is correct.

Problem 11 :

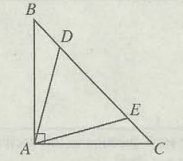
In the figure above, △ABC is an isosceles right triangle and △ADE is an equilateral triangle. If the measure of ∠EAC is x°, what is the value of x?

Solution:

∠BAD + ∠DAE + ∠EAC = 90°

x + 60° + x = 90°

2x + 60 = 90

2x = 30

x = 15°