PRACTICE PROBLEMS ON VOLUME OF 3D SHAPES

Problem 1 :

Find the volume of the cube

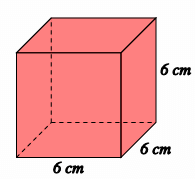
Solution :

Side length of the cube = 6 cm

Volume of cube = a³

= 6³

= 216 cm³

Problem 2 :

A cuboid has a length, width and height of 4 cm, 5 cm and 9 cm, respectively. Find the volume of the cuboid.

Solution :

Volume of cuboid = base area x height

length = 4 cm, width = 5 cm and height = 9 cm

= (4 x 5) x 9

= 20 x 9

= 180 cm³

Problem 3 :

Find the width of a cuboid, given that it has a length of 7 cm, height of 10 cm and volume of 490 cm³

Solution :

Volume = 490 cm³

length x width x height = 490 cm³

length = 7 cm and height = 10 cm

7 x w x 10 = 490

w = 490/(7 x 10)

w = 7 cm

So, the width is 7 cm.

Problem 4 :

Find its length, given that the volume of a cube is 343 cm³ 

Solution :

Side length = a

volume of cube = a³

a³ = 343

a = ∛343

a = ∛7 x 7 x 7

a = 7 cm

So, side length of the cube is 7 cm.

Problem 5 :

Find the volume of the triangular prism 

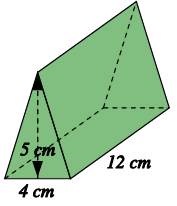
Solution :

Volume of the triangular prism = Area of triangle x height

Area of triangle = (1/2) x base x height

= (1/2) x 4 x 5

= 10 cm²

Volume of the triangular prism = 10 x 12

= 120 cm²

Problem 6 :

Find the volume of the trapezoidal prism

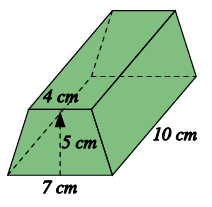
Solution :

Volume of trapezoidal prism = Area of trapezium x height

Area of trapezium = (1/2) x (sum of parallel sides) x height

= (1/2) (4 + 7) x 5

= (1/2) x 11 x 5

= 27.5 cm²

Volume of trapezoidal prism = 27.5 x 10

= 275 cm²

Problem 7 :

Find the volume of the square-based pyramid, rounding your answer to 3 significant figures

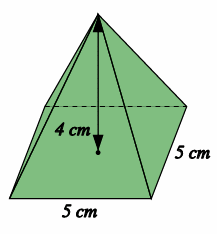
Solution :

Volume of pyramid = 1/3 x area of base x height

(1/3) x 5 x 5 x 4

= (1/3) x 100

= 33.3 cm³

Problem 8 :

Find the volume of the tetrahedron, rounding your answer to 3 significant figures

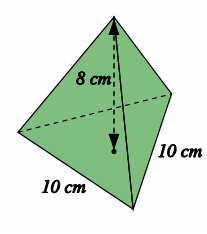
Solution :

Area of base = (√3/4) x a²

= (√3/4) x (10)²

= 25√3

Volume of tetrahedron = (1/3) x 25√3 x 8

= 115.46 cm³

Problem 9 :

Find the volume of the cone, rounding your answer to 3 significant figures

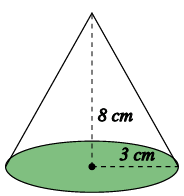
Solution :

Base area = πr²

= π(3)²

= 9π

Volume of cone = (1/3) x Base area x height

= (1/3) x 9π x 8

= 24π

= 24(3.14)

= 75.36

= 75.4 cm³

Problem 10 :

Find the volume of the sphere, rounding your answer to 3 significant figures

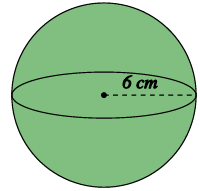
Solution :

Volume = (1/3) x base area x height

= (1/3)(4πr²) x r

= (1/3)(4π(6)²) x (6)

= (864/3)π

= 288π

= 904.32

= 904 cm³

Problem 11 :

A hemisphere has a radius of 2 cm. Find its volume, rounding your answer to 3 significant figures. 

Solution :

Volume = (1/3) x base area x height

= (1/3)(2πr²) x r

= (1/3)(2π(2)²) x (2)

= (16/3)π

= 5.3(3.14)

= 16.74 cm³

Problem 12 :

The solid shown below is a cuboid with a square-based pyramid on top. The pyramid has a vertical height of 4 cm. Find the volume of the solid, giving your answer to one decimal place where necessary.

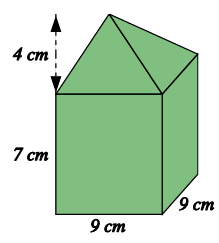
Solution :

Volume of the given shape = volume of top + volume of bottom

= 9 x 9 x 7 + (1/3)(9 x 9) x 4

= 567 + 108

= 675 cm³