PRACTICE PROBLEMS ON TRIGONOMETRIC FUNCTIONS

Problem 1 :

If tan θ = -1/√5, and θ lies in the IV quadrant, then the value of cos θ is

a) √5/√6     b) 2/√6     c) 1/2     d) 1/√6

Solution:

So, option (a) is correct.

Problem 2 :

The value of sin 765° is

a) √3     b) √3/2     c) 1/√3     d) 1/√2

Solution:

sin 765° = sin (720°+45°)

= sin 45°

sin 765° = 1/√2

So, option (d) is correct.

Problem 3 :

Range of cosine function is

a) R     b) (-∞, ∞)     c) (-1, 1)     d) [-1, 1]  

Solution:

The function f(x) = cos x has all real numbers in its domain, but its range is -1 ≤ cos x ≤ 1.

So, option (d) is correct.

Problem 4 :

Period of sine function is

a) π     b) 2π     c) 3π     d) 4π

Solution:

The period of the sine function is 2π, which means the value of the function is the same every 2π units.

So, option (b) is correct.

Problem 5 :

a) 1     b) -5     c) -1     d) 2

Solution:   

So, option (a) is correct.

Problem 6 :

The domain of sine function is

a) (-1, 1)     b) [-1, 1]     c) (0, ∞)     d) (-∞, ∞)

Solution:

Sine is an odd function and is periodic with period 2π . The sine function has a domain of all real numbers, and its range is -1 ≤ sin ⁡ x ≤ 1.

So, option (b) is correct.

Problem 7 :

Solution:

Problem 8 :

Domain of cosec x is _____

Solution:

cosec x will not be defined at the points where sin x is 0. Hence, the domain of cosec x will be R - nπ, where n ∈ I.

Problem 9 :

Solution: 

Problem 10 :

Solution:

Problem 11 :

Evaluate sin 180° + 3 cos 90° - 2 tan 45° + cosec 90°

Solution:

= sin 180° + 3 cos 90° - 2 tan 45° + cosec 90°

= 0 + 3(0) - 2(1) + 1

= -2 + 1

= -1

Problem 12 :

Solution:

Since 𝜃 lies in the third quadrant. Therefore, sin 𝜃 is negative and tan 𝜃 is positive.

Now,

Problem 13 :

Find the value of

a) cos 150°     b) tan 19π/3

Solution:

a) cos 150° 

cos 150° = cos (180° - 30°)

Angle lies in the second quadrant

= -cos 30°

= -√3/2

b) tan 19π/3

Values of tan x repeats after an interval of 2π, hence ignoring 3 × (2π).

Problem 14 :

Write the domain of i) sec x     ii) cot x

Solution:

i) sec x

Domain : 

{x | x ≠ .....-3𝜋/2, -𝜋/2, 𝜋/2, 3𝜋/2.....)

 ii) cot x

Domain : 

{x | x ≠ .....-2𝜋, -𝜋, 0, 𝜋, 2𝜋.....}

Problem 15 :

Draw the graph of sine function.

Solution:

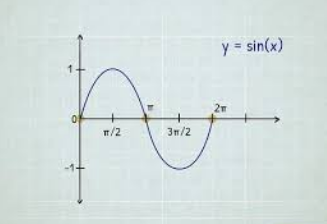
Problem 16 :

Draw the graph of cosine function. Also write its domain and range.

Solution:

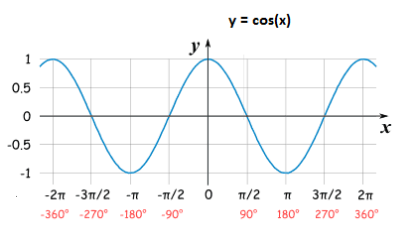
Domain :

All real numbers

Range :

-1 ≤ y ≤ 1