PRACTICE PROBLEMS ON TRIANGLES SIMILARITY

Problem 1 :

If △ABC ~ ARPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10 cm, then find QR.

Solution:

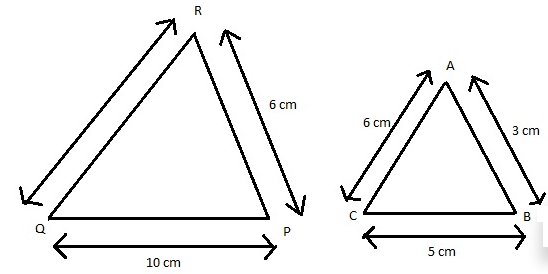
△ABC ≈ △RPQ

If two triangles are similar, then corresponding sides are proportional.

Problem 2 :

R and S are points on the sides DE and EF respectively of a ADEF such that ER = 5 cm, RD = 2.5 cm, SE = 1.5 cm and FS = 3.5 cm. Find whether RS || DF or not.

Solution:

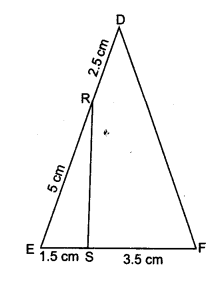
We have,

RE = 5 cm and RD = 2.5 cm

Similarity we have,

ES = 1.5 cm

SF = 3.5 cm

RS is not parallel to DF.

Problem 3 : 

In the figure, ABCD is a parallelogram and E divides BC in the ratio 1 : 3. DB and AE intersect at F. Show that DF = 4FB and AF = 4FE.

Solution:

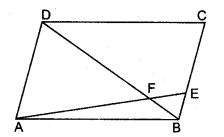
Given, ABCD is a parallelogram and BE : EC = 1 : 3

In △ADF and △EBF

∠ADF = ∠EBF (Alternate angles)

∠AFD = ∠EFB (Vertically opposite angle)

△ADF ~ △EBF (by alternate angle)

BC = BE + CE

= BE + 3BE

BC = 4BE

AD = BC

AD = 4BE

Put in (1), we get

Problem 4 :

In ADEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then the value of DB.

Solution:

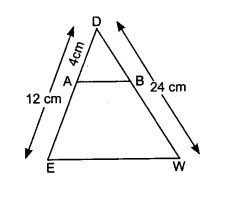
In △DEW, AB || EW

Problem 5 :

In figure, if ∠CAB = ∠CED, then prove that AB × DC = ED × BC.

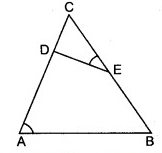
Solution:

Given, 

∠CAB = ∠CED

In △CAB and △CED

∠1 = ∠2

∠C = ∠C

So,

△CAB ~ △CED

Hence, it is proved.

Problem 6 :

In △ABC, from A and B altitudes AD and BE are drawn. Prove that △ADC ~ △AEB and △ADB ~ △ADC?

Solution:

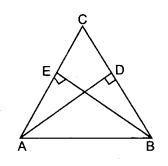
In △ADC and △BEC

∠D = ∠E

∠ACD = ∠BCE

So, △ADC ~ △BCE

△ADB is not similar to △AEB.

and △ADB is not similar to △ADC.

Problem 7 :

In △ABC, if ∠ADE = ∠B, then prove that △ADE ~ △ABC, if AD = 7.6 cm, AE = 7.2 cm, BE = 4.2 cm and BC = 8.4 cm, then find DE.

Solution:

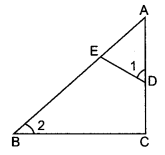
Given, 

∠ADE = ∠B (ie) ∠1 = ∠2

In △ADE and △ABC

∠1 = ∠2

∠A = ∠ A

△ADE ~ △ABC

Problem 8 :

If in an equilateral triangle the length of the median is √3 cm, then find the length of the side of equilateral triangle.

Solution:

Let a be the side of equilateral triangle. Median is also the altitude in an equilateral triangle.

Side of triangle = 2 cm.

Problem 9 :

In the figure, D and E are points on AB and AC respectively such that DE||BC. If AD = 1/3 BD and AE = 4.5 cm, find AC.

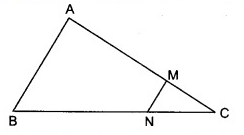
Solution:

Given,

DE||BC,

Problem 10 :

In the given figure, if LM || CB and LN || CD, prove that AM × AD = AB × AN.

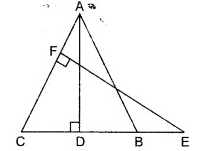
Solution:

In △BAC,

LM || BC

In △DAC,

LN || CD

From (1) and (2)

Hence, it is proved.

Problem 11 :

In the figure, PQR and SQR are two right triangles with common hypotenuse QR.  If PR and SQ intersect at M such that PM = 3 cm, MR = 6 cm and SM = 4 cm, find the length of MQ.

Solution:

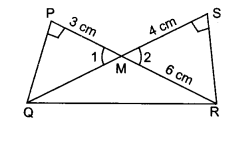
Consider the triangles MPQ and MSR.

∠P = ∠S

∠1 = ∠2

So, △MPQ ~ △MSR

Problem 12 :

In figure, DE || BC in AABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

Solution:

Given,, DE || BC

In △ADE and △ABC,

∠ADE = ∠ABC (corresponding angles)

∠A = ∠A

△ADE ~ △ABC

Problem 13 :

In figure, MN || AB, BC = 7.5 cm, AM = 4 cm and MC = 2  cm. Find the length BN.

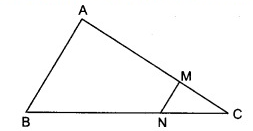
Solution:

In △ABC, MN || AB

△ABC ~ △MNC

Problem 14 :

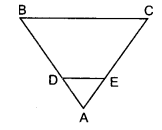
In figure, ABC is an isosceles triangle in which AB = AC. E is a point on the side CB produced, such that FE ⊥ AC. If AD ⊥ CB. Prove that AB × EF = AD × EC.

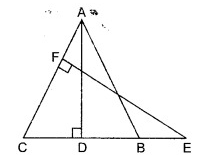
Solution:

In △ADB and △EFC,

∠D = ∠F and

∠B = ∠C (Angles opp to equal sides of a △ are equal)

△ABD ~ △ECF

AB × EF = AD × EC

Hence, it is proved.

Problem 15 :

The length of AB in the given figure:

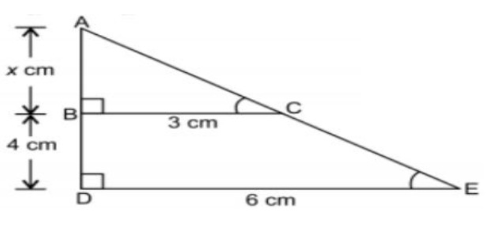
a) 8 cm       b) 6 cm           c) 4 cm     d) 10 cm

Solution:

By using BPT,

△ABC ~ △ADE

BC || DE

So, option (c) is correct.

Problem 16 :

In the figure, DE || BC. If AD = x, BD = x - 2, AE = x + 2 and EC = x - 1, find the value of x.

Solution:

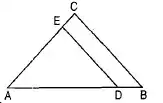
In △ABC, DE || BC

Problem 17 :

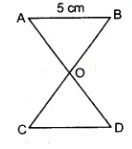
Solution:

In △AOB and △COD,

∠AOB = ∠COD (vertically opposite angles)

Therefore according to SAS similarity criterion, △AOB ~ △COD