PRACTICE PROBLEMS ON SETS AND RELATIONS FOR CA FOUNDATION

Problem 1 :

If the universal set is X = {x : x∈  1≤x ≤ 12} and A = {1, 9, 10}, B = {3, 4, 6 ,11, 12} and C = {2, 5, 6} are subsets of X then set A U(BnC) is

(a) {3, 4, 6, 12}    (b) {1, 6, 9, 10}

(c)  {2, 5, ,6, 11}     (d) None

Solution :

Given, A = {1, 9, 10}

B = {3, 4, 6 ,11, 12}

C = {2, 5, 6}

To find A U(BnC) :

BnC = {3, 4, 6, 11, 12} n {2, 5, 6}

BnC = {6}

A U(BnC) = {1, 9, 10} U {6}

A U(BnC) = {1, 6, 9, 10} 

So, option (b) is correct.

Problem 2 :

Out of 2000 employees in an office 48% preferred coffee(c), 54% liked tea(T), 64% used to smoke (S). Out of the total 28% used C and T, 32% used T and S and 30% preferred C and S, only 6% did none of these. The number having all the three is/

(a) 360       (b) 380     (c)  300    (d) None

Solution :

Total employees = 2000

n(C) = 48%

= (48/100) × 2000

= 960

n(T) = 54%

= (54/100) × 2000

= 1080

n(S) = 64%

= (64/100) × 2000

= 1280

 n(C n T ) = 28%

= (28/100) × 2000

= 560

n(T n S ) = 32%

= (32/100) × 2000

= 640

n(C n S ) = 30%

= (30/100) × 2000

= 600

n(C n S U T) = 6%

= (6/100) × 2000

= 120

 n(C U S U T) = 2000 - 120

= 1880

n(C U S U T) = n(C) + n(S) + n(T) - n(C n S) - n(S n T) - n(C n

T) + n(C n S n T) 

1880 = 960 + 1280 + 1080 - 600 - 640 - 560 + n(C n T n S) 

n(C n s n T) = 360 

Hence, number of people having all three is 360.

So, option (a) is correct.

Problem 3 :

If f(x) = x + 3 and g(x) = x² and (gof)(x) is 

(a) (x + 3)²     (b) x² + 3    (c)  x²(x + 3)    (d) None

Solution :

gof(x) = g(f(x))

= g(x + 3)

= (x + 3)²

So, option (a) is correct.

Problem 4 :

If f(x) = 1/(1 - x), then f^-1(x) is

(a) 1-x     (b) (x-1)/x   (c)  x/(x - 1)    (d) None

Solution :

f(x) = 1/(1 - x)

Let f(x) = y

y = 1/(1 - x)

y(1 - x) = 1

y - yx = 1

y - 1 = yx

x = (y - 1)/y

Interchange y and x.

Replace x with f^-1(x)

f^-1(x) = (x - 1)/x

So, option (b) is correct.

Problem 5 :

If f(x) = x + 3, g(x) = x² then fog(x) is 

(a) x²+ 3     (b) x² + x + 3    (c)  (x + 3)²    (d) None

Solution :

fog(x) = f(g(x))

= f(x²)

= x² + 3

So, option (a) is correct.

Problem 6 :

The number of subsets of the set {2, 3, 5}

(a) 3     (b) 8    (c)  6    (d) None

Solution :

Number of subsets = 2ⁿ

Where n is the number of elements in the set.

n = 3

∴ The number of subsets = 2³

= 8

So, option (b) is correct.

Problem 7 :

The null set is represented by 

(a)  Ø      (b) {0}    (c) {Ø}   (d) None

Solution :

The null set is represented by Ø.

So, option (a) is correct.

Problem 8 :

If P = {1, 2, 3, 5, 7} and Q = {1, 3, 6, 10, 15}, Universal set S = {1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15}

The cardinal number of PnQ is

(a)  3     (b) 2    (c) 0   (d) None

Solution :

P = {1, 2, 3, 5, 7}

Q = {1, 3, 6, 10, 15}

PnQ = {1, 3}

n(PnQ) = {2}

So, option (b) is correct.

Problem 9 :

At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. The number of women doctors attending the conference is.

(a)  2     (b) 4    (c) 1   (d) None

Solution :

Let M and D represent the set of indian men and doctors respectively.

From the information given in the question, we have

n(M) = 23, n(D) = 4, n(MUD) = 24

n(M U D) = n(M) + n(D) - n(M n D)

24 = 23 + 4 -  n(M n D)

24 = 27 - n(M n D) 

n(M n D) = 3

n(Indian men and doctors) = 3

number of women doctors = number of doctors - number of men doctors

= 4 - 3

= 1

So, the number of women doctors attending the conference is 1.

So, option (c) is correct.

Problem 10 :

Out of 150 students 45 passed in Accounts 50 in Maths. 30 in both Accounts and Maths. 32 in both Maths and costing 35 in both Accounts and Costing. 25 students passes in all the three subjects. Find the number who passes at least in any one of the subjects.

(a)  63     (b) 53    (c) 73   (d) None

Solution :

Number of students = 150

Passed in accounts = 45

Passed in maths = 50

Passed in cost = 30

Passed in accounts and maths = 30

Passed in maths and costing = 32

Passed in accounts and costing = 35

Passed in all three subjects = 25

= 45 + 50 + 30 - 30 - 32 - 35 + 25

 = 53

So, number of students passed in at least one subjects is 53.

Problem 11 :

f(x) = f(x - 1) + f(x - 2), if f(0) = 0, f(1) = 1, x = 2, 3, 4..... then what is f(7).

(a)  8     (b) 13    (c) 3   (d) 5

Solution :

Given, f(x) = f(x - 1) + f(x - 2)

`f(0) = 0 and f(1) = 1

f(2) = f(2 - 1) + f(2 - 2)

f(2) = f(1)

f(2) = 1

f(3) = f(3 - 1) + f(3 - 2)

f(3) = f(2) + f(1)

= 1 + 1

f(3) = 2

f(4) = f(4 - 1) + f(4 - 2)

f(4) = f(3) + f(2)

= 2 + 1

f(4) = 3

f(5) = f(5 - 1) + f(5 - 2)

f(5) = f(4) + f(3)

= 3 + 2

f(5) = 5

f(6) = f(6 - 1) + f(6 - 2)

f(6) = f(5) + f(4)

= 5 + 3

f(6) = 8

f(7) = f(7 - 1) + f(7 - 2)

= f(6) + f(5)

= 8 + 5

f(7) = 13

So, option (b) is correct.

Problem 12 :

f(x) = 2x³ + 1 then what is f-1(x) options

a)  1/2 (x - 1)^1/3     b) [(x - 1)/2]^1/3

c) [(x - 1)/2]^1/2        d) None

Solution :

f(x) = 2x³ + 1

Let f(x) = y

y = 2x³ + 1

y - 1 = 2x³

∛(y - 1)/2 = x

Interchange y and x.

Replace x with f^-1(x)

∛(x - 1)/2 = f^-1(x)

f^-1(x) = [(x - 1)/2]^1/3

So, option (b) is correct.

Problem 13 :

If A = {1,2,3,4,5,6,7,8,9,} B = {1,3,4,5,7,8};C = {2,6,8,} then find (A – B)UC =

(a) {2, 6}       (b) {2, 6, 8}     (c) {2, 6, 8, 9}   (d) None of these

Solution :

Given, A = {1,2,3,4,5,6,7,8,9}

B = {1,3,4,5,7,8}

C = {2,6,8}

To find (A – B)UC :

A - B = {1,2,3,4,5,6,7,8,9} - {1,3,4,5,7,8}

A - B = {2, 6, 9}

(A – B)UC = {2, 6, 9} U {2, 6, 8} 

(A – B)UC = {2, 6, 8, 9}

So, option (c) is correct.

Problem 14 :

If f (x) = x² and g(x) =√x then

(a) gof(3) = 3     (b) gof(–3) = 9

(c) gof(9) = 3     (d) gof(–9) = 3

Solution :

Given, f (x) = x² and g(x) =√x

(g o f)(x) = g(f(x))

= g(x²)

= (√x)²

(g o f)(x) = x

Let us consider option A).

(g o f)(3) = g(f(3))

= g(3²)

= (√3)²

(gof)(3) = 3 

Let us consider option B).

(g o f)(-3) = g(f(-3))

= g(-3²)

= (√-3)²

(g o f)(-3) = 9

So, option A) is correct. 

Problem 15 : 

A= {1, 2, 3, 4, ............... 10} a relation on A,

R = {(x, y)/x+ y =10, x ∈ A,y ∈ A,X ≥ Y} then Domain of R^–1 is

(a) {1, 2, 3, 4, 5}      (b) {0, 3, 5, 7, 9}

(c) {1, 2, 4, 5, 6, 7}    (d) None of these

Solution :

x + y = 10

Domain of R is range of R^-1

Range of R is domain of R^-1

When x = 1, y = 9

x = 2, y = 8....

x = 10, y = 0

Range of R is {0, 1, 2, .......9}

None of these is the answer.

Problem 16 :

 If A = {a, b, c, d}; B = {p, q, r ,s} which of the following relation is a function from A to B

(a) R₁= {(a, p), (b, q),(c, s)} (b) R₂ = {(a, p}, (b, r),(d, s)}

(c) R₃ = {(b, p),(c, s),(b, r)} (d) R₄ = {(a, p)(b, r)(c, q), (d, s)}

Solution :

Given, A = {a, b, c, d}; B = {p, q, r ,s}

Representing option (a) in arrow diagram.

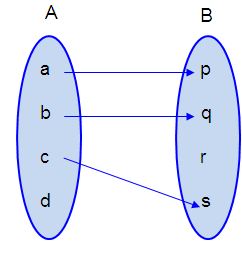
It is not a function.

Representing option (b) in arrow diagram.

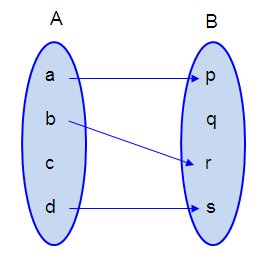
It is not a function.

Representing option (c) in arrow diagram.

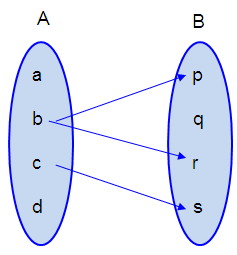
It is not a function.

Representing option (d) in arrow diagram.

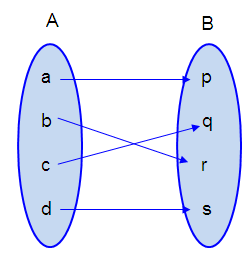
It is a function.

So, option (d) is correct.