PRACTICE PROBLEMS ON SAT

Problem 1 :

The radius of a circle is increased by 25%. By what percent does the area of the circle increase ?

Solution :

Let r be the radius of the circle.

Radius will increase 25% of the original.

Area of circle = πr²

Let old radius = r

New radius = r + 25% of r

= r + (25/100) r

= r + (1/4)r

= 5r/4

Problem 2 :

The length of a rectangle increased by 20%. The width is decreased by 20%. Which of the following accurately describes  the change in area of the following ?

(a)  Increases by 10%      (b)  Decreases by 10%

(c)  Decreases by 4%       (d)  Stays the same

Solution :

Let l and w be the length and width of rectangle respectively.

Area of rectangle = l x w

Length of the rectangle increased by 20%.

New length = 1.20l

New width = 0.80w

Area of new rectangle = 1.20l(0.80w)

= 1.20(0.80) lw

= 0.96 lw

= (96/100) lw

= 96 % of lw

area of new rectangle = 96% of old rectangle.

So, decrease of 4%.

Problem 3 :

F = 9q₁ q₂/r²

The force of attraction between two particles can be determined by the formula above, in which F is the force between them, r is the distance between them and q₁ and q₂ are charges of the two particles.

If the distance between two charged particles is doubled, the resulting force of attraction is what fraction of the original force ?

(a)  1/2    (b)  1/4   (c)  1/8       (d)  1/16

Solution :

New r = 2r

New force (F) = 9q₁ q₂/(2r)²

= 9q₁ q₂/4r²

= (1/4) (9q₁ q₂/r²)

So, the answer is 1/4.

Problem 4 :

P = V²/R

Electric power P is related to the voltage V and resistance R by the formula above. If the voltage were halved, how would the electric power be affected ?

(a)  The electric power would be 4 times greater

(b) The elevtric power would be 2 times greater

(c)  The electric power would be halved

(d)  The electric power would be quarter of what it was.

Solution :

P = V²/R

Voltage were halved, then new V = 1/2V

P = ((1/2)V)²/R

P = ((1/4)V)²/R

The electric power would be quarter of what it was.

Problem 5 :

Julie has a square fence that encloses her garden. She decides to expand her garden by making each side of the fence 10% longer. After this expansion, the area of Julie's garden will have increased by what percent ?

(a)  20%     (b)  21%     (c)  22%     (d) 25%

Solution :

Let x be the side length of garden.

Side length of new square = 110% of x

Area of square = (110% of x)²

= 1.21x²

Percentage increase = [(1.21x² - x²)/x²] • 100%

= (1.21 - 1) • 100%

= 0.21 • 100%

= 21%

Problem 6 :

A right circular cone has a base radius of r and a height of h. If the radius is decreased by 20% and height is increased by 10%, which of the following is the resulting percent change in the volume of cone ?

(a)  10% decrease    (b)  12% decrease 

(c)  18.4% decrease     (d) 29.6% decrease

Solution :

Volume of cone = πr²h

New radius = 80% of r

New height = 110% of h

Volume of new cone = π(0.80r)²(1.10h)

= 0.704πr²h

Percentage change = [(0.704πr²h - πr²h)/πr²h] • 100%

= [(0.704 - 1)πr²h)/πr²h] • 100%

= -0.296 • 100%

= -29.6 %

So, the answer is 29.6 % decrease.

Problem 7 :

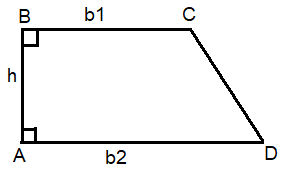
The area of the trapezoid above can be found using the formula (1/2)h(b₁+b₂). If lengths of BC and AD are halved and height is doubled, how would the area of the trapezoid change ?

(a)  The are would be increased by 50%

(b)  The area would stay the same

(c)  The area would be decreased by 25%

(d) The area would be decreased by 50%

Solution :

BC = b_1, New BC = b₁/2

AD = b_2, New AD = b₂/2

AB = h, New AB = 2h

Applying the values that we have received newly in the formula,

(1/2)h(b₁ + b₂)

we get, 

= (1/2)(2h)(b₁/2 + b₂/2)

= h(b₁/2 + b₂/2)

= (1/2)h(b₁+ b₂)

The area would stay same.

Problem 8 :

Calvin has a sphere that is four times bigger than the one Kevin has in terms of volume. The radius of Calvin's sphere is how many times greater in length than the radius of Kevin's sphere (rounded to the nearest hundredth) 

(a)  1.44    (b)  1.59    (c)  1.67    (d) 2.00

Solution :

Volume of sphere = (4/3)πr³

Let R be radius of Calvin's sphere and r be the radius of Kevin's sphere.

(4/3)πR³ = 4(4/3)πr³

(4/3)πR³ = 4(4/3)πr³

R³ = 4r³

R = ³√4r³

R = r (³√4)

Cube root of 4 is 1.59

R = 1.59 r

Problem 9 :

If a number p increased by 120 percent equals a number q decreased by 20 percent, which of the following is true?

(a)  q = (5/2)p   (b)  q = (11/4)p   

(c)  q = (7/2)p    (d) q = (15/4)p

Solution :

220% of p = 80% of q

220p = 80q

22p = 8q

11p = 4q

q = (11/4)p