PRACTICE PROBLEMS ON HINGE THEOREM

Refer to each figure given write an inequality relating the given pair of angle or segment measures.

Problem 1 :

m∠1, m∠2

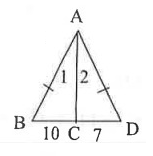
Solution :

m ∠ABD = m ∠ADB

The side which is opposite to m∠1 is 10.

The side which is opposite to m ∠2 is 7.

Then the relationship between m∠1 and m∠2 can be described as follows.

m ∠1 ____ m ∠2

The angle which is opposite to the longer side is larger.

m ∠1 > m ∠2

Problem 2 :

m < 1, m < 2

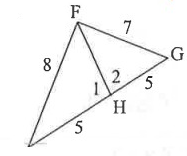
Solution :

By observing the figure,

The side which is opposite to m∠1 is 8.

The side which is opposite to m ∠2 is 7.

m∠1 ____ m∠2

The angle which is opposite to the longer side is larger.

So, m∠1 > m ∠2

Write an inequality or pair of inequalities to describe the possible values of x. Then solve the inequality to find the values of x.

Problem 3 :

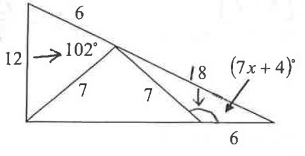
Solution :

Now comparison should be done with side lengths. 

18 > 12 or 12 < 18

Converse of Hinge theorem :

The angle which is opposite to larger measure is larger.

102 < 7x + 4

102 - 4 < 7x

98 < 7x

Dividing by 7 on both sides

98/7 < 7x/7

14 < x

Problem 4 :

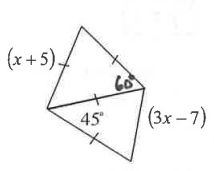
Solution :

The triangle which is at the top is equilateral and the triangle which is at below is called isosceles triangle.

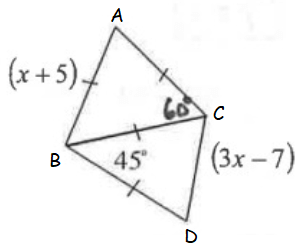
∠CBD = 45, ∠BCD = ∠BDC

∠BCD = (180 - 45)/2

∠BCD = 67.5

AB > CD

x + 5 > 3x - 7

5 + 7 > 3x - x

12 > 2x

12/2 > x

x < 6

Problem 5 :

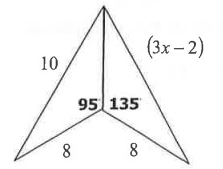
Solution :

The side which is opposite to 135 degree is greater side.

3x - 2 > 10

3x > 10 + 2

3x > 12

x > 12/3

x > 4

Problem 6 :

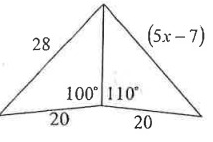
Solution :

110° is greater than 100°. So, the side which is opposite to 110° is greater side.

5x - 7 > 28

5x > 28 + 7

5x > 35

x > 35/5

x > 7

Problem 7 :

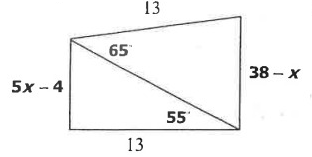
Solution :

Using converse of Hinge theorem, the side which is opposite to larger angle measure is larger.

38 - x > 5x - 4

38 + 4 > 5x + x

42 > 6x

42/6 > x

7 > x

Problem 8 :

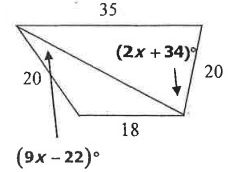
Solution :

Comparing the sides which is opposite to indicated angle measure 

35 > 18

2x + 34 > 9x - 22

34 + 22 > 9x - 2x

56 > 7x

x < 56/7

x < 8

Problem 9 :

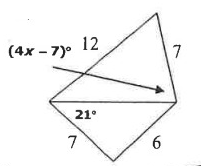
Solution :

The angle which is opposite to larger angle is larger.

12 > 7

4x - 7 > 21

4x > 21 + 7

4x > 28

x > 28/4

x > 7

So, the required value of x is 7.

Problem 10 :

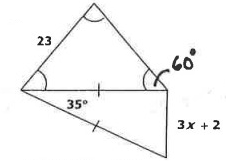
Solution :

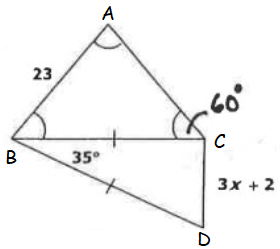
∠BCD = ∠BDC

∠BCD = (180 - 35)/2

∠BCD = 72.5

∠ACB > ∠CBD

3x + 2 > 23

3x > 23 - 2

3x > 21

x > 7

Problem 11 :

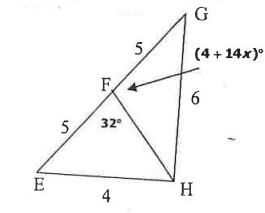
Solution :

Comparing the sides which is opposite to the indicated angle measure.

GH > EH

4 + 14x > 32

14x > 32 - 4

14x > 28

x > 28/14

x > 2