PRACTICE PROBLEMS ON GEOMETRY FOR SAT

Identify the choice that best completes the statement or answers the question.

Problem 1 :

If the measure of one of the angles in a parallelogram is z, what is the measure of an adjacent angle?

a. 180 - z      b. 360 - 2z    c. 360 - z    d. 180 - z/2

e. z

Solution:

One angle of parallelogram = z

Sum of adjacent angles of parallelogram = 180°

= 180 - z

So, option (a) is correct.

Problem 2 :

In the figure below, the measure of ∠A is 60°. If the measure of ∠B is twice the measure of ∠C, what is the measure of ∠C?

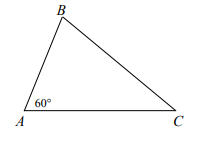
a. 120°   b. 40°    c. 90°       d. 80°      e. 20°

Solution:

∠A + ∠B + ∠C = 180°

60° + 2∠C + ∠C = 180°

3∠C = 180 - 60

3∠C = 120

∠C = 40°

So, option (b) is correct.

Problem 3 :

In the figure below, △QST is similar to △RSU. What is the length of RU?

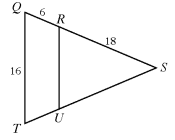
a. 10       b. 3/16      c. 64/3       d. 12         e. 16/3

Solution:

So, option (d) is correct.

Problem 4 :

In the figure below, what is the value of y in terms of x?

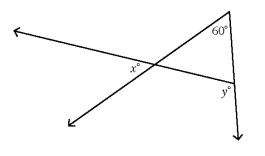
a. x + 60       b. 2x       c. 300 - x      d. 120 - x       e. x

Solution:

In the given figure, y is an exterior angle.

x and 60 is are interior angles of the triangle.

Exterior angle is equal to sum of two opposite interior angles.

y = x + 60

So, option (a) is correct.

Problem 5 :

In △ABC below, if AC = 10, then AB is equal to 

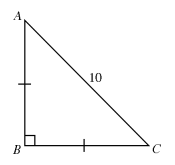
a. 5√2          b. 8        c. 2√5        d. 10√2      e. 5

Solution:

AB² + BC² = AC²

AB² + AB² = 10²

2AB² = 100

AB² = 50

AB = 5√2

So, option (a) is correct.

Problem 6 :

If one side of a triangle is three times as long as a second side, then the perimeter of the triangle could be:

a. 6x      b. 3x         c. 7x        d. 5x      e. 4x

Solution:

Let first side = x

Second side = 3x

Here the third side is unknown.

Third side > sum of length of two sides

The third side cannot be x.

If so, x + x > 3x is not true.

The third side cannot be 2x

x + 2x > 3x is not true

The third side can be 3x

x + 3x > 3x (true)

3x + 3x > x (true)

Then third side be 3x.

Perimeter = x + 3x + 3x

= 7x

So, option (c) is correct. 

Problem 7 :

In the figure below, ∠B and ∠D are right angles. What is the length of BC?

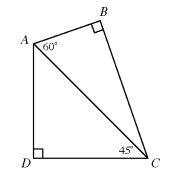
a. 2√6     b. 4√2       c. 2√2     d. 4√3      e. 2√3

Solution:

In 45 - 45 - 90 special right triangle,

Let DC = x

AC = √2 x

In 30 - 60 - 90 special right triangle,

AB = smaller side

Hypotenuse (AC) = 2 AB

√2 x = 2 AB

BC = √3 (smaller side)

BC = √3(√2 x/2)

= √6 (x/2)

If x = 4, then option a will be correct.

Problem 8 :

A parallelogram with two congruent adjacent sides must be a:

a. trapezoid       b. isosceles trapezoid     c. rectangle

d. square         e. rhombus

Solution:

A parallelogram with two congruent adjacent sides must be a rhombus.

Problem 9 :

In the figure below, line a is parallel to line b. Line c intersects both a and b with angles 1, 2, 3, 4, 5, 6, 7, and 8 as shown. Which of the following lists include all of the angles that are congruent to angle 6 ?

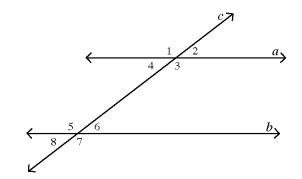
a. angles 5, 7, 3 and 1      b. angles 8, 4, and 3

c. angles 8, 4, and 2        d. angles 5, 7, and 3

e. angles 8, 7, and 4

Solution:

Angles 6 and 2 are corresponding angles.

2 and 4 are vertically opposite angles.

4 and 8 are corresponding angles.

congruent to angle 6 = 2, 4 and 8

So, option (c) is correct.

Problem 10 :

In the figure below, which pair of angles are supplementary?

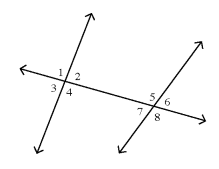
a. ∠3 and ∠7       b. ∠1 and ∠4        c. ∠5 and ∠7

d. ∠4 and ∠7       e. ∠2 and ∠5

Solution:

Supplementary angle ∠5 and ∠7

Problem 11 :

In the figure below, KL||NM. What is the length of LN?

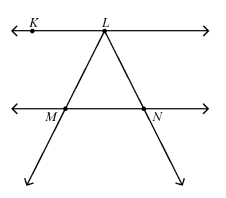
a. 10        b. 11        c. 12√2        d. 11

e. It cannot be determined from the given information.

Solution:

In the figure below, KL||NM, length of LN cannot be determined from the given information.

So, option (e) is correct.

Problem 12 :

In the figure below, quadrilateral PQRS is a parallelogram. If ∠SMR is a right angle, then x must be equal:

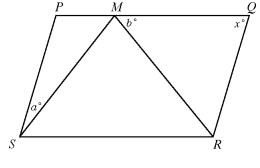
a. b        b. 90 + a        c. 90 - b     d. 90 + a - b

e. 90 - (a + b)

Solution:

∠SMR = 90

∠PMS + ∠MSP + ∠SPM = 180 -----(1)

In triangle PMS,

∠PMS + ∠SMR + ∠RMQ = 180

∠PMS + 90 + b = 180

∠PMS = 180 - 90 - b

∠PMS = 90 - b

Applying the value in (1), we get

90 - b + a + ∠SPM = 180

∠SPM = 180 - (90 - b + a)

∠SPM = 180 - 90 + b - a

∠SPM = 90 + b - a

Here ∠SPM  and ∠PQR are co-interior angles.

∠SPM + ∠PQR = 180

90 + b - a + x = 180

x = 180 - 90 - b + a

x = 90 - b + a

So, option (d) is correct.

Problem 13 :

Equilateral triangle ABC is inscribed in circle X. What is the measure of arc AB?

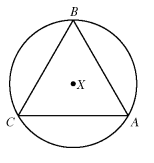
a. 30°      b. 60°     c. 90°      d. 120°    e. 240°

Solution:

Given that ABC is an equilateral triangle.

Each angle = 60°

∠A = ∠B = ∠C = 60°

arc AB = 2∠C

= 2 × 60

= 120°

So, option (d) is correct.

Problem 14 :

In the figure below, △LMN is an equilateral triangle. If LM is 4 units long, how many units long is arc MN?

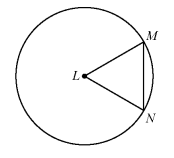
a. 8π/3    b. 4π/3    c. 2π/3    d. π/3    e. π

Solution:

Given, r = 4 units

𝜃 = 60°

So, option (b) is correct.