PRACTICE PROBLEMS ON FUNCTION NOTATION FOR SAT

Problem 1 :

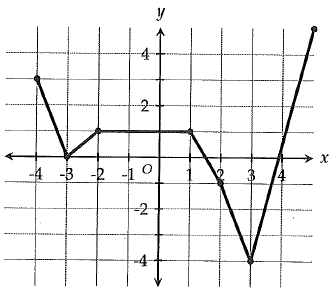
The graph above shows the function g. What is value of g(3) ?

a)  -4      b)   0     c) 3       d)  4

Solution

Problem 2 :

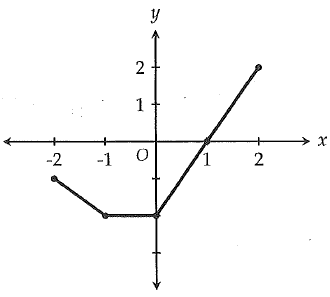
The graph of f(x) is shown in the xy plane above. If f(a) = -2, which of the following is a possible value of a.

a)  -1.5      b)   -0.5    c) 1       d)  2

Solution

Problem 3 :

The function f is defined by f(x) = (1/2)x + a, where a is constant. If f(a) = 3, what is the value of f(8) ?

Solution

Problem 4 :

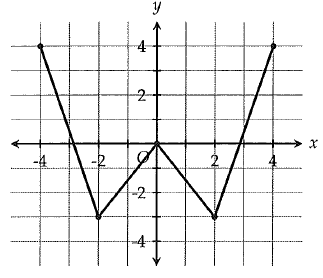
The complete solution f is shown in the xy plane. If f(x) = k has two solutions, which of the following could be the value of k ?

I)  -3       II) 0      III)  2.5

a)  I and II     b)  III only     c)  I and III only     d)  I, II and III

Solution

Problem 5 :

p(t) = -t² + 16t + k

The price of a stock on day number t can be modeled by the function p above, where k is a constant and 1 ≤ t ≤ 15. On what number day was the price of the stock equal to what it was on day number 3 ?

a)    9       b)  11       c)  13      d)   15

Solution

Problem 6 :

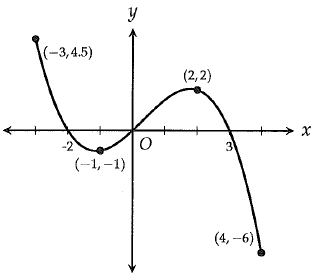
The function y = f(x), defined for -3 ≤ x ≤ 4 is graphed in the xy plane above. Which of the following gives all values of x for which f(x) is negative ?

a)  -3 ≤ x ≤ 4      b)  -2 < x ≤ 4

c)  -2 < x < 0 and 3 < x ≤ 4

d)  -3 ≤ x < -2 and 0 < x < 3

Solution

Problem 7 :

The functions f and g are defined by

f(x) = x² + 2 and g(x) = 4x - 3.

If a > 0, for what value of a does g(f(a)) = 41 ?

Solution

Problem 8 :

v = 550 - 9.8t

The equation above gives the velocity v of a ball t seconds after it is thrown vertically upwards with an initial velocity of 550 meters per second. After approximately how many seconds will the ball stop and start drop back to the ground ?

a)  47.8    b)  51.4       c)  55.5     d)  56.1

Solution

Problem 9 :

If f(x + 1) = 3x + 2, the function f could be defined by which of the following ?

a)  f(x) = 3x - 2      b)  f(x) = 3x - 1

c)  f(x) = 3x + 1      d)  f(x) = 3x + 5

Solution

Problem 10 :

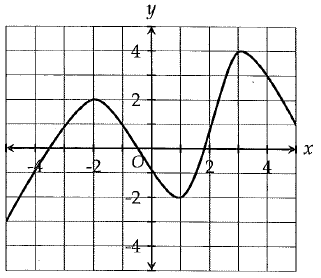
What is the difference between the minimum and maximum values of the function graphed in the xy plane for -5 ≤ x ≤ 5 ?

Solution

Problem 11 :

A function f(x) has two properties

f(a + b) = f(a) - b

f(2) = 10

What is the  value of f(5) ?

a)  5     b)  7     c)  9       d)  11

Solution

Problem 12 :

f(x) = x + 2, if x ≥ 0

f(x) = x - 2, if x < 0

The function f is defined above. Which of the following cannot be f(x) for any value of x ?

a)  -6      b)  -4     c)  1    d) 3

Solution

Problem 13 :

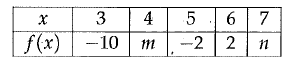
The values in the table above define a linear function. What is the value of m + n ?

a)  -4     b) 0     c)  4        d)  8

Solution