PRACTICE PROBLEMS ON CIRCLES FOR SAT

Problem 1 :

In the figure above, BD is a diameter, and PA and PD are tangents to circle O. m∠CDE = 52 and m∠APD = 45 and AP = 9.

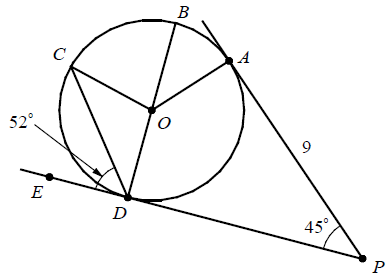
1)  What is the measure of ∠ODC ?

2)  What is the measure of ∠OCD ?

3)  What is the measure of ∠AOD ?

4)  What is the length of PD ?

Solution :

(1) A line drawn from center of circle to the tangent line will be a perpendicular.

So,

∠ODE = 90

∠ODC + ∠CDE = 90

∠ODC + 52 = 90

∠ODC = 90 - 52

∠ODC =  38

(2)  Since OC and OD are radius, they are having same measures and they will create equal angles.

∠OCD =  38

(3)  Considering the quadrilateral AODP,

Sum of interior angles of a quadrilateral = 360

OD and OA are perpendiculars to PD and PA.

So, 90 + 90 + ∠AOD + ∠DPA = 360

180 + ∠AOD + 45 = 360

∠AOD = 360 - 225

∠AOD = 135

(4) Length of PD is also 9.

Because the tangents drawn from an external point to a circle are equal.

Problem 2 :

In the figure given below O is inscribed in triangle PQR. If PA = 12, QA = 6 and RB = 9.5. What is the perimeter of triangle PQR ?

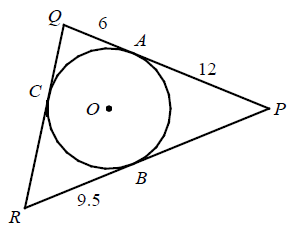
Solution :

RB = RC = 9.5

PB = PA = 12

QC = QA = 6

Perimeter of triangle PQR :

= PQ + QR + PR  ----(1)

PQ = PA + AQ ==> 12 + 6 ==> 18

PR = PB + BR ==> 12 + 9.5 ==> 21.5

RQ = RC + QC ==> 9.5 + 6==> 15.5

Applying the values in (1), we get

= 18 + 21.5 + 15.5

= 55

Problem 3 :

A certain pizza restaurant cuts slices out at every 4 inches along the edge of a pizza, as shown in the figure below. What is maximum number of of full pizza slices that can be cut out from a circular pizza with a radius of 10 inches ?

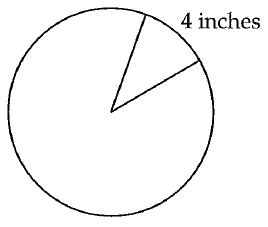
Solution :

Length of arc = 4 inches = piece of pizza having arc length

Number of pizzas = Perimeter of the circular pizza / 4

= 2πr/4

= [2(3.14) 10]/4

= 15.7

So, 15 pizzas can be cut out.

Problem 4 :

In the figure given below, circle A has a radius of 2, circle B has a radius of 4, the circle C has a radius of 6. what is the area of the shaded region ?

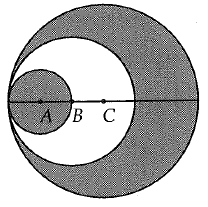
Solution :

Area of small circle having center at A.

Radius of circle having center A is 2 units.

Area of small circle = πr²

= π(2)²

= 4π

Area of remaining part (shaded)

= Area of circle having center C - Area of circle having center B

= π6² - π4²

= π(36-16)

= 20π

Sum of shaded portions = 4π + 20π

= 24π

Problem 5 :

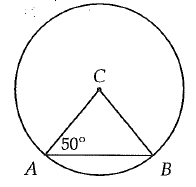
In the figure given above, A and B are points on the circle C. If the area of the circle is 54π, what is the area of the sector formed by the central angle ACB ?

Solution :

Area of the circle = 54π

πr² = 54π

r² = 54

r = √54

r = 3√6

The given triangle ACB is a isosceles triangle, because CA and CB are equal(radii)

∠ACB = 80