PRACTICE MATH PROBLEMS PRECALCULUS 

Problem 1 :

Evaluate the function at the given value of the independent variable and simplify.

f(x) = x² - 5 ; f(x - 4)

Solution :

Given, f(x) = x² - 5

Substitute x = x - 4 the given equation.

f(x - 4) = (x - 4)² - 5

= x² + 16 - 2(x)(4) - 5

= x² + 11 - 8x

∴ f(x - 4) = x² + 11 - 8x

Problem 2 :

Use the graph to find the indicated function value.

y = f(x), Find f(-2)

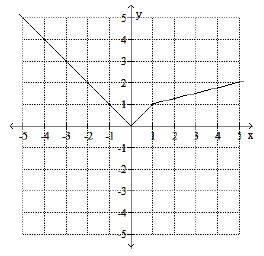
Solution :

y = f(x)

f(-2) = ?

f(-2) is the value of the function.

x is equal to -2.

By observing the figure.

f(-2) = 2

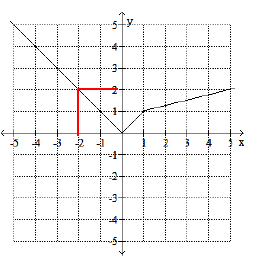
Problem 3 :

Use the graph to determine the function's domain and range.

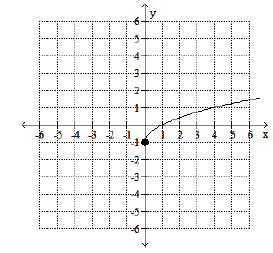
Solution :

The domain is all possible values of x, horizontally the graph starts from 0 and continues upto ∞.

The range is all possible values of y, horizontally the graph starts from -1 and continues upto ∞.

Domain = [0, ∞)

Range = [-1, ∞)

Problem 4 :

Use the graph of the given function to find any relative maxima and relative minima. State where f(x) increases and decreases.

f(x) = x³ - 3x² + 1

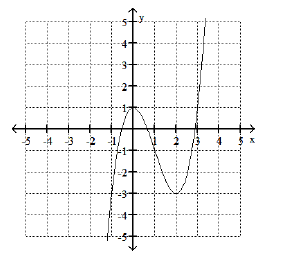
Solution :

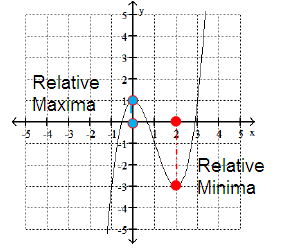
Relative maxima = (0, 1)

Relative minima = (2, -3)

f(x) is increases in (-∞, 0) ∪ (2, ∞)

f(x) is decreases in (0, 2)

Problem 5 :

Find and simplify the difference quotient [f(x + h) - f(x)]/h, h ≠ 0 for the given function.

f(x) = x² + 7x + 3

Solution :

f(x) = x² + 7x + 3  

f(x + h) =(x + h)² + 7(x + h) + 3

= x² + h² + 2(x)(h) + 7x + 7h + 3

Problem 6 :

Use the given conditions to write an equation for the line in slope - intercept form.

Passing through (2, 5) and (1, 8)

Solution :

(2, 5) = x₁, y₁

(1, 8) = x₂, y₂

m = (y₂ - y₁)/(x₂ - x₁)

= (8 - 5)/(1 - 2)

= 3/-1

m = -3

Passing through the point (2, 5) = (x, y)

y = mx + b

5 = (-3)(2) + b

5 = -6 + b

b = 5 + 6

b = 11

y = -3x + 11

Problem 7 :

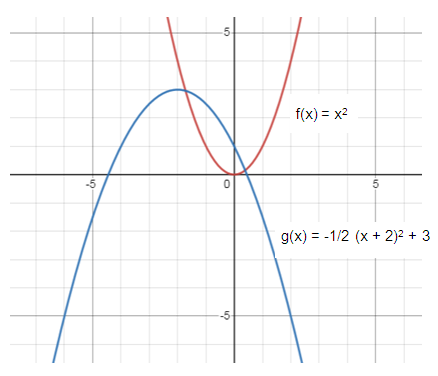
Begin by graphing the standard quadratic function f(x) = x². Then use transformations of this graph to graph the given functions.

g(x) = -1/2 (x + 2)² + 3

Solution :

Given, f(x) = x².

g(x) = -1/2 (x + 2)² + 3

For f(x), the vertex is V(0, 0), symmetric about y-axis and open upward parabola.

g(x) = -1/2 (x + 2)² + 3

Reflection about x-axis, vertical shrink with the factor of 1/2 units, horizontal translation of 2 units left and vertical translation of 3 units up.

Problem 8 :

For the given functions f and g, find the indicated composition.

(f ∘ g) (x)

Solution :

(f ∘ g) (x) = f(g(x))

(f ∘ g) (x) = 35x/(20x + 4)

Problem 9 :

Find the inverse of the one - to - one function.

f(x) = 3/(2x + 1)

Solution :

Given, f(x) = 3/(2x + 1)

Let f(x) = y

y = 3/(2x + 1)

Put x = y and y = f^-1(x)

x = 3/(2y + 1)

Problem 10 :

Complete the square and write the equation in standard form. Then give the center and radius of the circle.

x² - 10x + 25 + y² - 8y + 16 = 64

Solution :

Given, x² - 10x + 25 + y² - 8y + 16 = 64

x² - (5)(2)x + 5² + y² - (4)(2)y + 42 = 64

(x - 5)² + (y - 4)² = 64

(x - 5)² + (y - 4)² = 8²

Comparing with (x - h)² + (y - k)² = r²

Center = (5, 4)

Radius = 8