POPULATION GROWTH AND DECAY WORD PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Exponential Word Problems: Growth & Decay
Growth Formula: y = a (1 + r)t
Decay Formula: y = a (1 – r)t
where a = original number
r = rate (% in decimal form)
t = time periods
Write an exponential function to model each situation. Find each amount at the end of the specified time. Round your answers to the nearest whole number.
Problem 1 :
A town with a population of 5,000 grows 3% per year. Find the population at the end of 10 years.
Solution :
y = a(1 + r)t
Here a = initial population, r = increasing rate and t = number of years
Initial population = 5000
Increasing rate = 3% and
number of years = 10
y = 5000(1 + 3%)10
y = 5000(1 + 0.03)10
y = 5000(1.03)10
y = 5000(1.344)
y = 6720
Problem 2 :
The population of Boomtown is 475,000 and is increasing at a rate of 3.75% each year. When will the population exceed 1 million people (to the nearest year)?
Solution :
Initial population = 475,000
Increasing rate = 3.75%
y = a(1 + r)t
475000(1 + 3.75%)t > 1000000
475000(1 + 0.0375)t > 1000000
Dividing by 475000 on both sides.
(1 + 0.0375)t > 2.105
(1.0375)t > 2.105
To solve use equal sign, we get
t log(1.0375) = log(2.105)
t(0.015) = 0.323
t = 0.323/0.015
t = 21.53
So, it will take 21 years tp reach the population of 1 million.
Problem 3 :
The population of Leave town is 123,000 and is decreasing at a rate of 2.375% each year.
• When will the population of Leave town drop below 50,000 (to the nearest year)?
• What will the population of Leave town be 100 years from now?
Solution :
(i) y = a(1 - r)t
Initial population = 123000
When will the population become below 50000.
123000(1 - 2.375%)t < 50000
Divide by 123000 on both sides.
(1 - 0.02375)t < 0.4065
(0.97625)t < 0.4065
Take log on both sides, we get
t log (0.97625) < log (0.4065)
t(-0.0104) < -0.3909
t < 0.3909/0.0104
t < 37.58
So, it will take 38 years.
(ii) y = a(1 - r)t
After 100 years the population will be.
y = 123000(1 - 2.375%)100
y = 123000(0.97625)100
y = 123000(0.09038)
y = 11118
Problem 4 :
Problem The 1989 population of Mexico was estimated at 87,000,000. The annual growth rate is 2.4%. When will the population reach 100,000,000 (to the nearest year)?
Solution :
Population is increasing, so we will use the formula
y = a(1 + r)t
Initial population = 87000000
Growth rate = 2.4%
After how many year the population will become 100,000,000.
87000000(1 + 2.4%)t = 100,000,000.
(1 + 0.024)t = 100,000,000/87000000
(1 + 0.024)t = 100,000,000/87000000
(1.024)t = 1.149
Taking log on both sides, we get
log (1.024)t = log (1.149)
t log(1.024) = log(1.149)
t = log(1.149)/log(1.024)
t = 0.0603/0.0102
t = 5.911
So, the population will become 100,000,000 after 6 years.
Problem 5 :
The population of Small town in the year 1890 was 6,250. Since then, it has increased at a rate of 3.75% each year.
a) What was the population of Small town in the year 1915?
a) In 1940?
c) What will the population of Small town be in the year 2003?
d) When will the population reach 1,000,000 (to the nearest year)?
Solution :
Population is increasing :
y = a(1 + r)t
(a) Initial population a = 6250, increasing rate = 3.75%
Population will be at 1915 :
Difference in years = 1915 - 1890 ==> 25 years
y = 6250(1 + 3.75%)25
y = 6250(1 + 0.0375)25
y = 6250(1.0375)25
y = 6250(2.510)
y = 15688
(b) In 1940 :
Difference between 1940 and 1890
= 1940-1890
= 50 years
y = 6250(1 + 3.75%)50
y = 6250(1.0375)50
y = 6250(6.3)
y = 39380
So, at 1914 the population will be 39380.
c) Population at 2003 :
= 2003 - 1890
= 113
y = 6250(1.0375)113
y = 6250(64.07)
y = 400438.
(d) After how many the population will be become 1,000,000
1,000,000 = 6250(1 + 3.75%)t
Dividing by 6250 on both sides.
160 = (1.0375)t
log 160 = t log (1.0375)
2.204 = t(0.015)
t = 2.204/0.015
t = 146.9
t = 147
After 147 years, the population will be 1,000,000.
Problem 6 :
You have a checking account and a money market account at a local bank. Your checking account has a constant balance of $200. The table shows the total balance of the accounts over time.
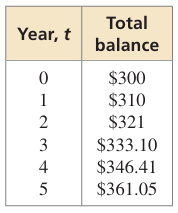
a. Write a function m that represents the balance of your money market account after t years.
b. Write a function B that represents the total balance after t years. Compare the graph of m to the graph of B.
Solution :
The $200 balance of your checking account can be represented by the constant function c(t) = 200. To find the balances m(t) of the money market account, subtract $200 from each value in the table, as shown.
From this table, you know the initial balance is $100, and it increases 10% each year.
So, P = 100 and r = 0.1
m(t) = P(1 + r)t
= 100(1 + 0.1)t
b. To write a function that represents the total balance, find the sum of the expressions that represent the balances of the two accounts.
B(t) = m(t) + c(t)
= 100(1.1)t+ 200
From the graphs, you can see that the graph of B is a vertical translation of the graph of m.

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling