PLOTTING POLAR COORDINATES

Plot the point with the given polar coordinates.

Problem 1 :

(-2,  3π/4)  

Solution :

When we have negative radius, we can roughly plot with the positive radius and make the reflection line of it to get the original.

Here we see polar graph. In between 0 to π/2, we see 6 portions. so each portion will be 15 degree or π/12

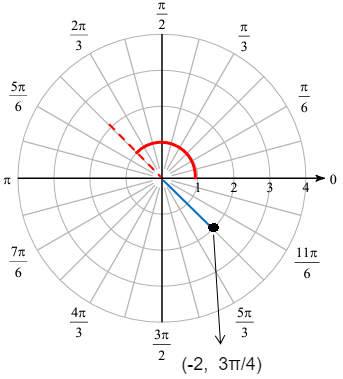
Since we have negative radius, we do the reflection. 

Problem 2 :

(3, 150°)

Solution :

Both r and θ are positive. So, we have to do counter clockwise rotation 

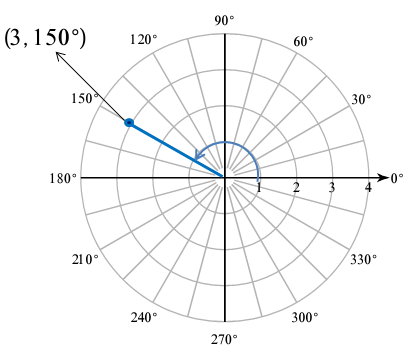
Problem 3 :

(2, -225°)

Solution :

Here r is positive and angle measure is negative. So, we have to do clock wise rotation.

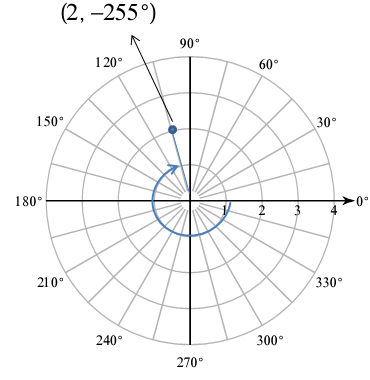
Problem 4 :

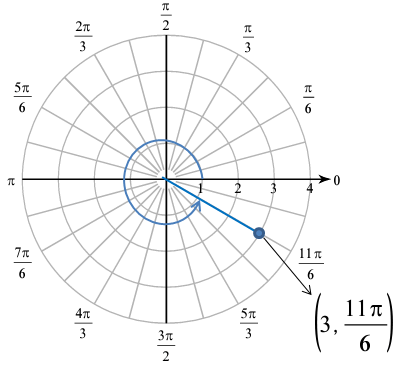
(3, 11π/6)

Solution :

Here r and angle measure both are positive. So, we have to do counter clockwise rotation, and mark the point.

Problem 5 :

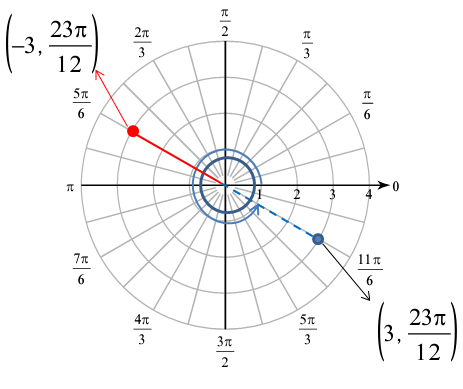
(-3, 23π/12)

Solution :

Here r and angle measure both are positive. So, we have to do counter clockwise rotation, and mark the point.

Problem 6 :

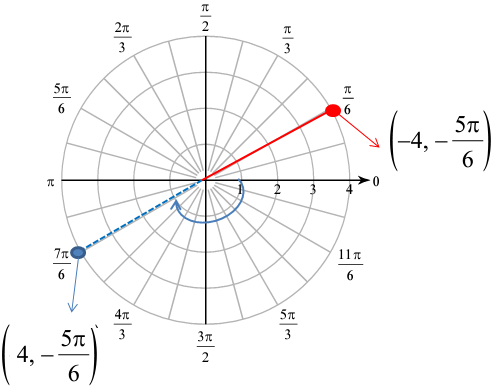
(-4, -5π/6)

Solution :

Here r is negative, then we have to do the reflection. Theta is negative, so we have to do clockwise rotation.

Problem 7 :

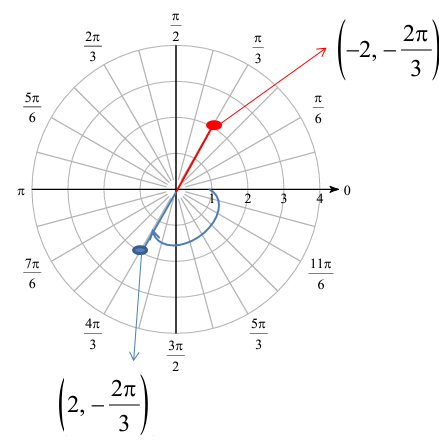
(-2, -2π/3)

Solution :

Here r is negative, then we have to do the reflection. Theta is negative, so we have to do clockwise rotation.

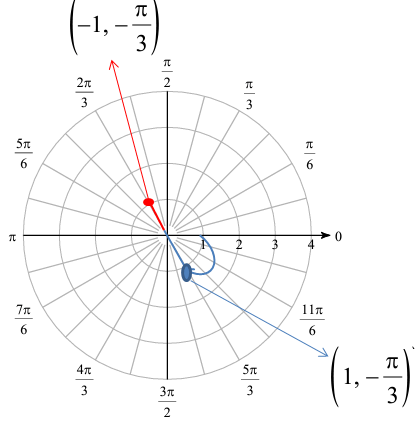
Problem 8 :

(-1, -π/3)

Solution :

Here r is negative, then we have to do the reflection. Theta is negative, so we have to do clockwise rotation.