PLOTTING IRRATIONAL NUMBERS ON A NUMBER LINE
To plot irrational numbers on the number line, we have to memorize some of the following values given below.
|
√1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 |
√36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 |
For example,
√27
The approximate value of √27 is 5....., because
√25 < √27 <√36
So, in the number line, in between 5 and 6, we have to mark it.
What is rational number ?
All numbers that can be written in the form of p/q is rational number.
What are irrational numbers ?
The numbers that cannot be written in the form of fraction, those are irrational numbers.
For example,
√2, √3, √5, .......etc are examples of irrational numbers.
Consider, √4, √9, √25 ....... etc
these are not irrationals, because
√4 = √(2 x 2) ==> 2
Since we can write it as fraction, it cannot be irrational. It is rational.
Place a point on the number line given for each of the following irrational numbers.
Problem 1 :
Point A :√2

Solution :
Point A :√2
√2 lies between √1 and √3.
Approximate value of √2 is 1.414.
So, the point 1.414 lies between 1.0 and 1.5.
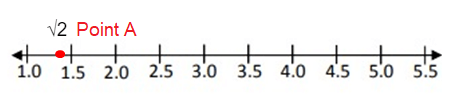
Problem 2 :
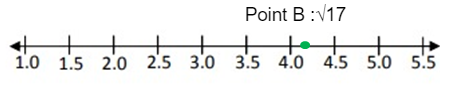
Point B :√17

Solution :
Point B :√17
√17 lies between √16 and √25.
Approximate value of √17 is 4.1.
So, the point 4.1 lies between 4 and 4.5.
Problem 3 :
Point C :√11

Solution :
Point C :√11
√11 lies between √9 and √16.
Approximate value of √11 is 3.3....
So, the point 3.3 lies between 3.0 and 3.5.

Problem 4 :
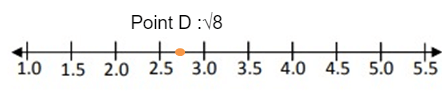
Point D :√8

Solution :
Point D :√8
√8 lies between √2 and √9 and it is more nearer to √9.
Approximate value of √8 is 2.8
So, the point 2.8 lies between 2.5 and 3.0.
Problem 5 :
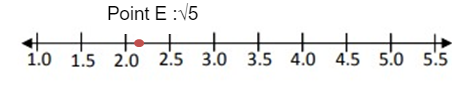
Point E :√5

Solution :
√5 lies between √2 and √9.
Approximate value of √5 is 2.24.
So, the point 2.24 lies between 2.0 and 2.5.
Problem 6 :
Point V :√26

Solution :
Point V :√26
√26 lies between √25 and √36.
Approximate values of √26 is 5.1....
So, the point 5.1 lies between 5.0 and 5.5.
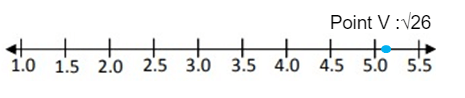
Problem 7 :
Point W :√88

Solution :
Point W : √88
√88 lies between √81 and √100.
Approximate value of √88 is 9.38.
So, the point 9.4 lies between 9.0 and 9.5.
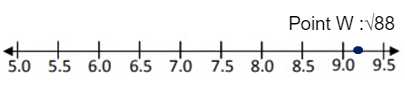
Problem 8 :
Point X :√77

Solution :
Point X :√77
√77 lies between √64 and √81.
Approximate value of √77 is 8.7.
So, the point 8.7 lies between 8.5 and 9.0.
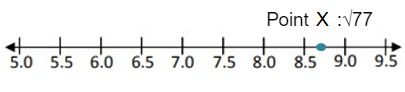
Problem 9 :
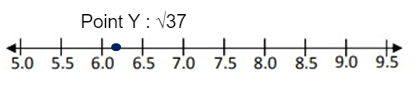
Point Y :√37

Solution :
Point Y : √37
√37 lies between √25 and √36.
Approximate value of √37 is 6.1
So, the point 6.1 lies between 6.0 and 6.5.
Problem 10 :
Point Z :√30

Solution :
Point z :√30
√30 lies between √25 and √36.
Approximate values of √30 is 5.3
So, the point 5.3 lies between 5.0 and 5.5.
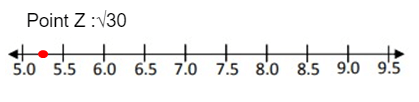
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling