PERPENDICULAR BISECTOR THEOEREM OF A TRIANGLE

If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment.

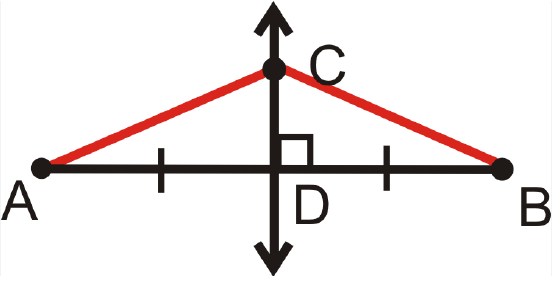
Consider two triangles, ADC and BCD.

∠ADC = ∠BDC (90 degree angle)

AD = BD (Bisector)

CD = CD (Common)

By CPCTC (Corresponding parts congruence triangle)

AC = BC

Problem 1 :

Find the measure of RT and RV.

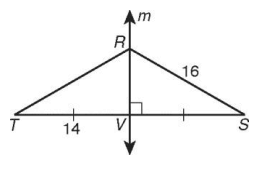
Solution :

In triangle RTV and RVS.

∠RVT = ∠RVS (90°)

TV = VS (Bisector)

RV = RV (Common)

By CPCTC

TR = 16

TR² = TV² + VR²

16² = 14² + VR²

VR² = 256 - 196

VR² = 60

VR = √60

VR = 2√15

Problem 2 :

Find the measure of HJ

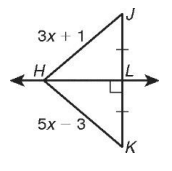
Solution :

Here HL is perpendicular bisector,

In triangle HLJ and HLK.

∠HLJ = ∠HLK (90°)

LJ = LK (Bisector)

HL = HL (Common)

By CPCTC

HJ = HK

3x + 1 = 5x - 3

3x - 5x = -3 - 1

-2x = -4

x = 2

Applying the value of x, we get

HJ = 3(2) + 1

HJ = 7

Problem 3 :

Find the measure of FG.

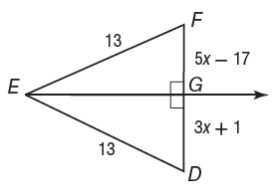
Solution :

FG = GD

5x - 17 = 3x + 1

5x - 3x = 1 + 17

2x = 18

x = 9

Applying the value of x, we get

FG = 5(9) - 17

FG = 45 - 17

FG = 28

Problem 4 :

Find x and y.

a) m∠ADB = (7x + 27), find x

b) BC = (3y – 7), BD = (y + 3). Find y.

Here AD is perpendicular bisector.

Solution :

a)

m∠ADB = (7x + 27)

m∠ADB = 90

7x + 27 = 90

7x = 63

x = 63/7

x = 9

b) BC = (3y – 7), BD = (y + 3)

Since AD is perpendicular bisector, BD = DC

2BD = BC

2(y + 3) = 3y - 7

2y + 6 = 3y - 7

2y - 3y = -7 - 6

-y = -13

y = 13

Problem 5 :

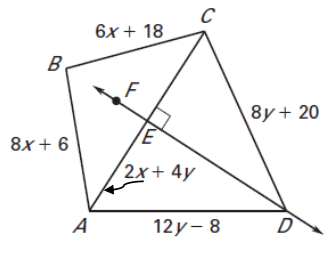
DE is the perpendicular bisector of AC.

Solution :

Since DE is perpendicular bisector, AE = EC

In triangles AED and DEC,

AD = DC

12y - 8 = 8y + 20

12y - 8y = 20 + 8

4y = 28

y = 7

In triangles ABE and BEC,

AB = BC

8x + 6 = 6x + 18

8x - 6x = 18 - 6

2x = 12

x = 12

Problem 6 :

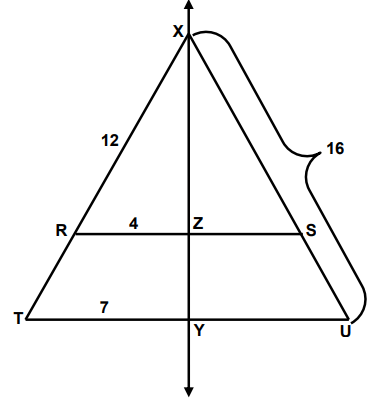
XY is perpendicular bisector of RS and TU

Solution :

XU = XS + SU

XS = 12 = XR

16 = 12 + SU

SU = 16 - 12

SU = 4

i) XS = 12

ii) XT = 16

iii) TU = TY + YU

= 7 + 7

TU = 14

iv) ZS = 4 = RZ

v) TR = 4 = SU

Problem 7 :

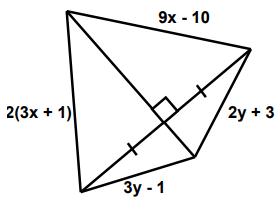
use the diagrams to solve for the unknown variables x and y.

Solution :

Problem 8 :

CD is the Perpendicular Bisector of AB If

AC = 6x + 9 and CB = 2x + 33

find BC.

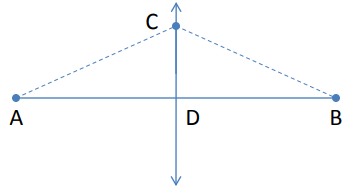
Solution :

AC = BC

6x + 9 = 2x + 33

6x - 2x = 33 - 9

4x = 24

x = 24/4

x = 6

Applying the value of x.

BC = 2(6) + 33

= 12 + 33

= 45