PARALLEL LINES CUT BY A TRANSVERSAL

Transversals creates three important types of angles, namely:

1. Corresponding angles

2. Co-interior angles

3. Alternating angles

Corresponding angles are in the same position as each other.

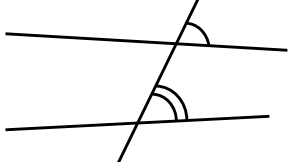
Co-interior angles are between the lines and on the same side of the transversal. They are “inside together”.

Alternate angles are between the lines and on alternate (opposite) sides of the transversal.

Vertically opposite angles :

When two straight lines intersect the angles opposite each other are called vertically opposite angles.

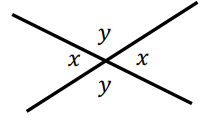
Vertically opposite angles are equal to each other.

Problem 1 :

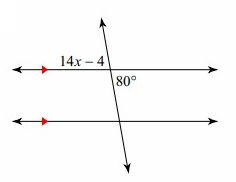
Solution:

Lines are parallel. So, vertical angles are equal.

14x - 4 = 80°

14x = 84

x = 6

Problem 2 :

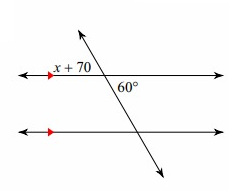
Solution:

x + 70 = 60°

x = 60 - 70

x = -10

Problem 3 :

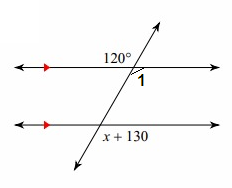
Solution:

∠1 and x + 130° are corresponding angles. So, they will be equal.

∠1 = x + 130° and

∠1 = 120° (Vertically opposite angles)

x + 130° = 120°

x = -10

Problem 4 :

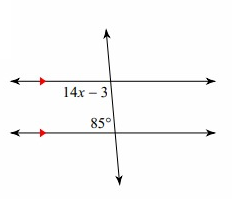
Solution:

85 and 14x - 3 are co-interior angles. So, they add upto 180°.

85 + (14x - 3) = 180°

85 + 14x - 3 = 180°

82 + 14x = 180°

14x = 180 - 82

14x = 98

x = 7

Problem 5 :

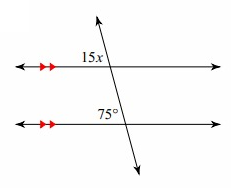
Solution:

15x and 75° are corresponding angles.

15x = 75°

x = 5

Problem 6 :

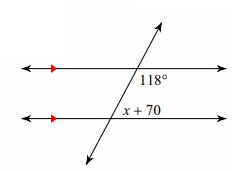
Solution:

118 and x + 70 are co-interior angles, so they will be equal.

118 + x + 70 = 180°

188 + x = 180°

x = 180 - 188

x = -8

Problem 7 :

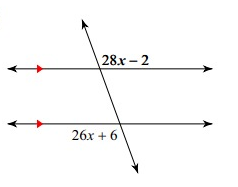
Solution:

28x - 2, 26x + 6  are alternate exterior angles.

28x - 2 = 26x + 6

28x - 26x = 6 + 2

2x = 8

x = 4

Problem 8 :

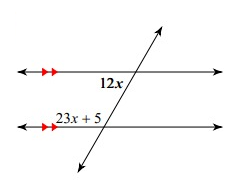
Solution:

12x and 23x + 5 are co-interior angles.

23x + 5 + 12x = 180°

35x + 5 = 180°

35x = 175

x = 175/35

x = 5

Problem 9 :

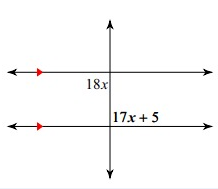
Solution:

18x = 17x + 5 (alternate interior angles are equal)

18x - 17x = 5

x = 5

Problem 10 :

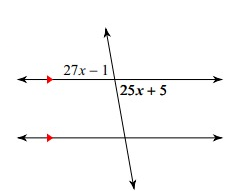
Solution:

27x - 1 and 25x + 5 are vertically opposite angles, they will be equal.

27x - 1 = 25x + 5

27x - 25x = 5 + 1

2x = 6

x = 6/2

x = 3