ORDER THE SIDE LENGTHS OF THE TRIANGLE FROM SHORTEST TO LONGEST

Problem 1 :

In ∆ABC, m∠A = 90, m∠B = 55 and m∠C = 35.

a) List the sides in order from smallest to largest.

b) Classify the triangle by its sides.

Solution:

a) Order the angles from smallest to longest :

35, 55, 90

The side opposite to the smallest angle is the shortest side and the side opposite to the largest angle is the longest side.

side opposite to 35 ----> AB

side opposite to 55 ----> AC

side opposite to 90 ----> BC

Order of the sides from smallest to largest:

AB < AC < BC

b) All three sides are different. So it is scalene triangle.

Problem 2 :

In ∆ABC, m∠B = 140 and m∠C = 20.

a) List the sides in order from smallest to largest.

b) Classify the triangle by its angles.

Solution:

a)  In ∆ABC, 

m∠A + m∠B + m∠C = 180˚

Substitute m∠B = 140˚ and m∠C = 20˚

m∠A + 140 + 20 = 180˚

m∠A + 160 = 180˚

m∠A = 180 - 160

m∠A = 20˚

m∠B = 140˚ and the remaining two angles m∠A and m∠C are equal, that is 20˚.

side opposite to m∠A ----> BC

side opposite to m∠B ----> AC

side opposite to m∠C ----> AB

In ∆ABC, the longest side is AC and the remaining two sides BC and AB are equal in length.

b)   In the triangle, two of the angles are congruent. So, it is isosceles obtuse triangle.

Problem 3 :

In ∆PQR, PQ = 8, QR = 12, and RP = 13.

a) List the angles in order from smallest to largest.

b) Classify the triangle by its sides.

Solution:

a)  Order the sides from smallest to largest:

8, 12, 13

The angle opposite to the shortest side is the smallest angle and the side opposite to the longest side is the largest angle.

angle opposite to the side 8 long ----> ∠R

angle opposite to the side 12 long ----> ∠P

angle opposite to the side 13 long ----> ∠Q

Order of the angles from smallest to largest:

 ∠R < ∠P < ∠Q

b)  All three sides are different. So it is scalene triangle.

Problem 4 :

In ∆ABC, measure of ∠ACB = 70˚ and the measure of ∠ABC = 65˚

a) List the sides in order from smallest to largest.

b) Classify the triangle by its angles.

Solution:

a)  In ∆ABC, 

m∠BAC + m∠ABC + m∠ACB = 180˚

Substitute m∠ACB = 70˚ and m∠ABC = 65˚

m∠BAC + 65 + 70 = 180˚

m∠BAC + 135 = 180˚

m∠BAC = 180 - 135

m∠BAC = 45˚

Order of the angles from smallest to largest:

45˚ < 65˚ < 70˚

side opposite to 45˚ ----> BC

side opposite to 65˚ ----> AC

side opposite to 70˚ ----> AB

Order of the sides from smallest to largest:

BC < AC < AB

b)

i. All the three angles are different.

ii. Each of the three angles is less than 90˚.

So, the triangle is a scalene and acute triangle.

Problem 5 :

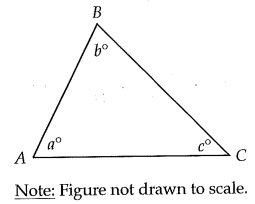
The triangle above is isosceles and b > a. Which of the following must be FALSE ?

a)  AB = BC     b)  AB = AC     c)  AC = BC     d) a = c

Solution :

Comparing angles a and b, b is greater than a.

Option a :

There is a chance to be AB = BC, when a = c.

Option b :

There is a chance to be AB = AC, when b = c.

Option c :

There is a chance to be AC = BC, when a = b, but it is not true. Since we have the evidence b > a, AC > BC.

So, option c is FALSE.

Problem 6 :

As shown in the diagram below of ABC, BC is extended through D, m∠A = 70, and m∠ACD = 115

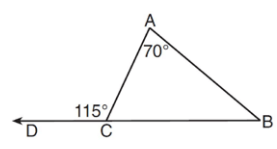
Which statement is true?

a) AC > AB      b) AB > BC      c) BC < AC      d) AC < AB

Solution :

m∠ACD = 115 (Exterior angle)

Sum of remote interior angle = 115

m∠A + m∠B = 115

70 + m∠B = 115

m∠B = 115 - 70

m∠B = 45

m∠C = 180 - 115

m∠C = 65

Ordering angles from least to greatest :

m∠B < m∠C < m∠A

Ordering sides from least to greatest :

AC < AB < BC

Hence AC < AB is true.

Problem 7 :

In ABC, m∠A = 60, m∠B = 80, and m∠C = 40. Which inequality is true?

a) AB > BC     b) AC > BC      c) AC < BA     d) BC < BA

Solution :

Ordering angles from least to greatest :

m∠C < m∠A < m∠B

Ordering sides from least to greatest :

AB < BC < AC

Hence AC > BC is true.

Problem 8 :

In triangle ABC, m∠B < m∠A < m∠C. Which statement is false?

a) AC > BC     b) BC > AC     c) AC < AB      d) BC < AB

Solution :

Given relationship :

m∠B < m∠A < m∠C

Ordering sides from least to greatest :

AC < BC < AB

Considering option a, AC is greater than BC.

Problem 9 :

∆XYZ is an isosceles triangle with equal angles 1 and 2 shown. Find :

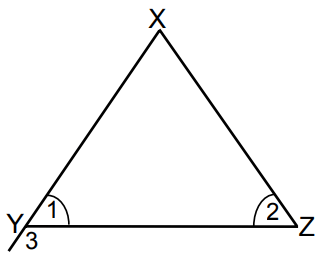
a) the size of ∠2 if ∠X = 56°.

b) the size of ∠3.

c) the longest side of ∆XYZ.

Solution :

a)  ∠X + ∠Y + ∠Z = 180

56 + ∠1 + ∠2 = 180

∠1 + ∠1 = 180 - 56

2∠1 = 124

∠1 = 124/2

∠1 = 62 = ∠2

b)  

∠1 + ∠3 = 180

62 + ∠3 = 180

∠3 = 180 - 62

∠3 = 118

c)  XY and XZ will have the same measure.

Problem 10 :

∆RST is isosceles with angles S and T equal. ∠R = 40°.

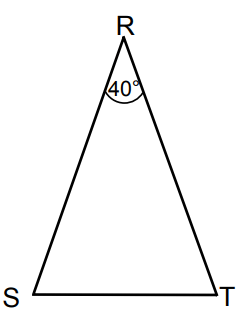
a) What is the size of ∠S?

b) What is the shortest side of ∆RST?

Solution :

∠S + ∠R + ∠T = 180

∠S + 40 + ∠S = 180

2∠S = 140

∠S = 70

In the triangle above ∠R is smallest, then ST is the smallest side.