OPTIMIZATION WORD PROBLEMS CALCULUS WORKSHEET

Problem 1 :

When a small business employs x workers to manufacture its goods, the profit made is given by

P(x) = -2x³ + 2400 x - 4000 euros per week.

a) How many employees should they use to maximise profit ?

b) What is the maximum profit ?

Solution

Problem 2 :

Square corners are cut from a piece of 12 cm by 12 cm tinplate which is then bent to form an open dish. What size squares should be removed to maximise the capacity of the dish ?

Solution

Problem 3 :

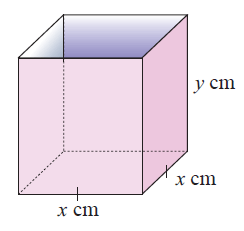
An open rectangular box has a square base, and its outer surface area must be 108 cm²

a) Find the equation in terms of x and y.

b) Write y in terms of x.

c) Find the formula for the capacity C in terms of x and y.

d) What size must the base be in order to maximise the capacity ?

Solution

Problem 4 :

The slant edge of the cone has length 12 cm. If the cone has height x cm, find 

a) an expression for the volume of the cone in terms of x.

b) The value of x for which the cone has the maximum possible volume.

Solution