NC MATH 1 EOC REVIEW PACKET WITH SOLUTIONS

Problem 81 :

The equations 5x + 2y = 48 and 3x + 2y = 32 represent the money collected from school concert ticket sales during two class periods. If x represents the cost for each adult ticket and y represents the cost for each student ticket, what is the cost for each adult ticket?

A. $20          B. $10           C. $8         D. $4

Solution:

Let x be an adult ticket

y be a student ticket

5x + 2y = 48 ---> (1)

3x + 2y = 32 ---> (2)

(2) × -1 ==> -3x - 2y = -32

Adding (1) & (2), we get

2x = 16

x = 8

The cost for each adult ticket is $8.

So, option (C) is correct.

Problem 82 :

A. x²            B. x⁹          C. 4x²             D. 4x⁹

Solution:

So, option (C) is correct.

Problem 83 :

The pressure exerted on the floor by a person's shoe heel depends on the weight of the person and the width of the heel. The formula is

where P is pressure in pounds per square inch, W is weight in pounds, and H is heel width in inches. Which of the following shows the pressure formula solved for H?

Solution:

So, option (B) is correct.

Problem 84 :

Which inequality is represented by the graph below?

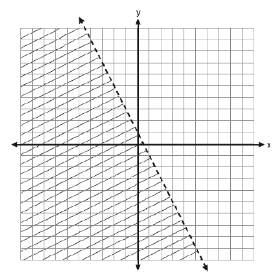
Problem 85 :

The area of a parallelogram is 35p⁶q⁶ square units. If the base of the parallelogram measures 5pq² units, what is the height of the parallelogram? (p > 0 and q > 0)

A. 7p⁵q⁴ units           B. 7p⁶q³ units

C. 30p⁵q⁴ units        D. 30p⁶q³ units

Solution: 

A = Bh

Let h be the required height.

35p⁶q⁶ = 5pq² h

h = 35p⁶q⁶ / 5pq²

h = 7p⁵q⁴ units

So, option (A) is correct.

Problem 86 : 

The cost of renting a van for one day includes a flat rental fee plus a charge for each mile the van is driven while it is rented. A van that is driven 107 miles costs $97.15. A van that is driven 127 miles costs $106.15. What is the flat rental fee?

A. $19         B. $20          C. $45           D. $49

Solution:

Lets call the flat rental fee b.

x is a charge for each mile.

107x + b = 97.15 ---> (1)

127x + b = 106.15 ---> (2)

Subtract (1) from (2), we get

20x = 9

x = 9/20

Put x = 9/20 in (1)

107(9/20) + b = 97.15

48.15 + b = 97.15

b = 97.15 - 48.15

b = $49

So, option (D) is correct.

Problem 87 :

At a linen sale Mrs. Earle bought twice as many pillowcases for $2 each as sheets for $5 each. If she spent less than $40, not including tax, what is the maximum number of pillowcases she could have purchased?

A. 3          B. 4          C. 6           D. 8

Solution:

p = 2s

2p + 5s = 40

2(2s) + 5s < 40

4s + 5s < 40

9s < 40

s < 40/9

s < 4.44

s = 4

p = 2(4)

p = 8

So, option (D) is correct.

Problem 88 :

The gas tank in Mina's car holds 15 gallons. Her car gets between 25 and 30 miles to the gallon. Of Mina fills up the gas tank and then drives until she runs out of gas, what is the least number of miles she can drive?

A. 300 mi         B. 375 mi         C. 405 mi       D. 450 mi

Solution:

If her car gets 25 miles per gallon, the least number of miles she can drive is 25 miles per gallon multiplied by the number of gallons in the gas tank which is 15 gallons.

So, 15 × 25 = 375 mi

So, option (B) is correct. 

Problem 89 :

The population of Williston is currently 15,400 people. If the population at an average rate of 325 people per year, which equation could be sued to find the approximate number of years it will take for the population to reach 18,000 people?

A. 15,400 + 325n = 18,000                B. 325n = 18,000

C. 15,400n + 325 = 18,000               D. 15,400n = 18,000

Solution:

15400 + 325n = 18000

So, option (A) is correct.

Problem 90 :

To which of the following situations can the function y = 5x + 10 best be applied?

A. The number of miles a person walks if he walks for 5 hours at the rate of 10 miles per hour.

B. The total weight on a scale if 5 pounds is placed there initially and a series of 10-pound weights are added to it.

C. The total wages earned by a waiter who is paid $5 per hour and earns $10 in tips.

D. The combined length of 5 boards, each 10 feet longer than the width of a doorway.

Solution:

Option A :

Let x be the number of miles the person can walk.

Walks for 5 hours at 10 miles per hour

Number of miles = 5 × 10 = 50 miles

Option B :. 

Initial weight on scale = 5 pound

Let 10 pound weights added be x.

and total weight on scale be y.

y = 10x + 5

Option C :

Tip = $10

Earning = $5/hour

Let number of hours be x.

Let total wage be y.

y = 5x + 10

Option D :

Number of Boards = 5

Dimensions = 10 + x, where x = width of doorway

Let combined length be y

y = 5(10 + x)

So, option (C) is correct.