NC MATH 1 EOC PRACTICE TEST ONLINE WITH SOLUTIONS

Problem 61 :

Which is an equation of a line that is parallel to line MN?

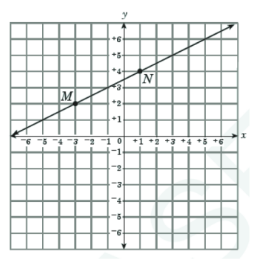
A. 2x - y = 3               B. x - 2y = 3

C. 8x + 4y = 4           D. 9x + 18y = -9

Solution:

Slope = Rise / run

M(-3, 2) and N(1, 4)

m = (4 - 2) / (1 + 3)

= 2/4

= 1/2

So, option (B) is correct.

Problem 62 :

Solution:

So, option (D) is correct.

Problem 63 :

A long string with a balloon at the end was tied to the ground. After a breeze came up, the balloon was 55 feet to the right of where it was tied and 30 feet above the ground, as shown in the figure below. 

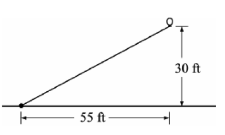
What is the slope of the line between the balloon and the point where it was tied?

Solution:

So, option (A) is correct.

Problem 64 :

The distance traveled by a marble on a flat table as it rolls in a straight line is determined by the formula:

Where

s = Distance traveled      u = Initial Velocity

t = Time elapsed            a = Acceleration

Which of the following shows the distance traveled formula solved for a?

Solution:

So, option (A) is correct.

Problem 65 :

A computer is purchased for $1,200 and depreciates at $140 per year. Which linear equation represents the value, V, of the computer at the end of t years?

A. V = 1,200 - 140t        B. V = 140t

C. 140t - 1,200             D. V = 140(1,200 - t)

Solution:

V = 1,200 - 140t

1200 is the original value, and if you are depreciating, the value goes down, hence the minus.

So, option (A) is correct.

Problem 66 :

Which equation is equivalent to 5x - 2(7x + 1) = 14x?

A. -9 - 2x = 14x           B. -9x + 1 = 14x

C. -9x - 2 = 14x          D. 12x - 1 = 14x

Solution:

5x - 2(7x + 1) = 14x

5x - 14x - 2 = 14x

-9x - 2 = 14x

So, option (C) is correct.

Problem 67 :

At a local grocery store, watermelons are sold for $4 each plus an additional $0.25 per pound. Write a function that describes the relationship between x, the number of pounds of a watermelon, and f(x), the total cost of the watermelon.

A. f(x) = 4.25x                    B. f(x) = 4 + 0.25x

C. f(x) = 4(0.25 + 1)          D. f(x) = 4x(0.25x + 4)

Solution:

If x is the number of pounds of a watermelon.

Then the total cost of the watermelon is 4 + 0.25x.

So, option (B) is correct.

Problem 68 :

A group of 3 children and 2 adults pay a total of $120 to take a karate class. A group of 5 children and 1 adult take the same karate class for $95. What is the total cost for 1 child and 1 adult to take the karate class?

A. $60          B. $55        C. $51         D. $48

Solution:

Let x be a child and y be an adult.

3x + 2y = 120 ---> (1)

-2(5x + y = 95)

-10x - 2y = -190 ---> (2)

Adding (1) & (2),

-7x = -70

x = 10

By applying x = 10 in (1)

3(10) + 2y = 120

30 + 2y = 120

2y = 90

y = 45

Total cost for 1 child and 1 adult to take the karate class = 10 + 45

= $55

Problem 69 :

Find an equation for the line with y-intercept 3 that is perpendicular to the line 3y = 2x - 4. 

A. 2y = 6 - 3x               B. 2y = 3x + 6

C. 3y = 9 - 2x              D. 3y = 2x + 9

Solution:

For perpendicular lines m₁m₂ = -1

When, m₁ = slope of first line

m2 = slope of second line

3y = 2x - 4

y = 2x/3 - 4/3

m₁ = 2/3

m₁m₂ = -1

(2/3)m₂ = -1

m₂ = -3/2

y = mx + b

when x = 0, y = 3

3 = m(0) + b

b = 3

y = (-3/2)x + b

2y = -3x + b

2y = 6 - 3x

So, option (A) is correct.

Problem 70 :

Which is the line parallel to the line y = 8x - 2?

A. y = 2x - 8                    B. y = -1/8x + 3

C. y = 4 + 8x                 D. 2y = 8x + 3

Solution:

y = 8x - 2

Because the line is parallel to y = 8x - 2.

So, the slope is equal to 8.

So the line is y = 4 + 8x.

So, option (C) is correct.