MULTIPLYING BINOMIALS

To multiply binomials which are in the form of

(x+a) (x+b)

we will follow the steps given below.

• Multiply x by (x+b). 
• Multiply a by (x+b)

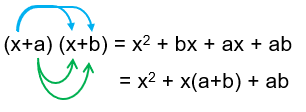
Expand the following and simplify :

Problem 1 :

(x + 2) (x + 5)

Solution :

By distributing x and 2, we get

= (x ∙ x) + (x ∙ 5) + (2 ∙ x) + (2 ∙ 5)

= x² + 5x + 2x + 10

By combining like terms.

= x²+7x+10 

Problem 2 :

(x - 3) (x + 4)

Solution :

By distributing x and -3, we get

= (x ∙ x) + (x ∙ 4) + (-3 ∙ x) + ( -3 ∙ 4)

= x² + 4x - 3x - 12

By combining like terms.

= x² + x - 12 

Problem 3 :

(x - 2) (x - 10)

Solution :

By distributing x and -2, we get

= (x ∙ x) - 10 (x) + (-2)x + (-2) (-10)

= x²  -10x - 2x + 20

By combining like terms.

= x² - 12x + 20

Problem 4 :

(2x + 1) (x - 3)

Solution :

By distributing 2x and 1, we get

= (2x ∙ x) + 2x (-3) + 1x + 1(-3)

= 2x² - 6x + x - 3

By combining like terms.

= 2x² - 5x - 3

Problem 5 :

(2x + y) (x - y)

Solution :

By distributing 2x and y, we get

= (2x ∙ x) + (2x)(-y) + (y ∙ x) + (y) (-y)

= 2x² - 2xy + xy - y²

By combining like terms.

= 2x² - xy - y²

Problem 6 :

(x + 3) (-2x - 1)

Solution :

By distributing x and 3, we get

= x(-2x) + x (-1) + 3 (-2x) + (3) (-1)

= -2x² - x - 6x - 3

By combining like terms.

= -2x² - 7x - 3

Multiplying Binomials to Get Difference of Two Squares

Expand and simplify :

Problem 7 :

(x + 7) (x - 7)

Solution :

By distributing x and 7, we get

= (x ∙ x) + x ( -7) + (7 ∙ x) + 7 (-7)

= x² -7x + 7x - 49

By combining like terms.

= x² - 49

By observing the binomial given above, they are almost same except the signs. Instead of multiplying the binomials directly, we can use algebraic identity 

(a + b) (a - b) = a² - b²

(x + 7) (x - 7) = x² - 7²

= x² - 49

Problem 8 :

(3 + a)(3 - a)

Solution :

By distributing 3 and a, we get

= (3 ∙ 3) + 3(-a) + a(3) + a(-a)

= 9 - 3a + 3a - a²

By combining like terms.

= 9 - a²

Alternative Method :

(a + b) (a - b) = a² - b²

(3 + a) (3 - a) = 3² - a²

= 9 - a²

Problem 9 :

(2x + 1) (2x - 1)

Solution :

By distributing 2x and 1, we get

= (2x) (2x) + (2x) (-1) + 1 (2x) + 1 (-1)

= 4x² - 2x + 2x - 1

By combining like terms.

= 4x²-1

Alternative Method :

(a + b) (a - b) = a² - b²

(2x + 1) (2x - 1) = (2x)² - 1²

= 4x² - 1

Problem 10 :

(4 - 3y) (4 + 3y)

Solution :

By distributing 4 and -3y, we get

= (4 ∙ 4) + (4 ∙ 3y) + 4(-3y) + (-3y) (3y)

= 16 + 12y - 12y - 9y²

By combining like terms.

= 16 - 9y²

Problem 11 :

5(3x + c) = 15x + 40

Solution :

5(3x + c) = 15x + 40

Using distributive property, we get 

15x + 5c = 15x + 40

By equating the corresponding terms, we get

5c = 40

c = 40/5

c = 8

So, the value of c is 8.

Problem 12 :

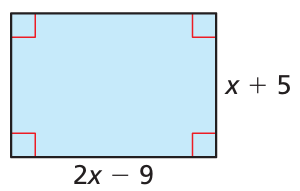
Write a polynomial that represents the area of the shaded region.

Solution :

Length = 2x - 9 and width = x + 5

Area of rectangle = length ⋅ width

= (2x - 9)(x + 5)

= 2x(x) + 2x(5) - 9(x) - 9(5)

= 2x² + 10x - 9x - 45

= 2x² + x - 45

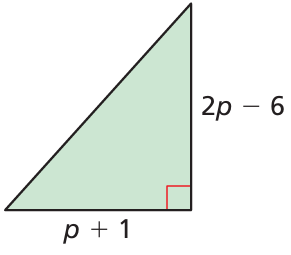
Problem 13 :

Solution :

Base = p + 1 and height = 2p - 6

Area of triangle = (1/2) ⋅ base ⋅ height

= (1/2) (p + 1)(2p - 6)

= (1/2) (2p² - 6p + 2p - 6)

= (1/2) (2p² - 4p - 6)

= (2p² - 4p - 6)/2

= p² - 2p - 3

So, area of triangle is p² - 2p - 3.

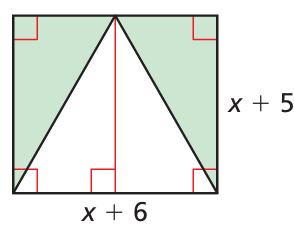
Problem 14 :

Solution :

By observing the figrue, we have triangle inscribed inside the rectangle.

Dimensions of rectangle :

Length = x + 6 and width = x + 5

Dimensions of triangle :

Base = x + 6 and height = x + 5

Area of shaded region = Area of rectangle - area of traingle

= (x + 6)(x + 5) - (1/2)(x + 6)(x + 5)

= (1/2)(x + 6)(x + 5)

= (1/2)(x² + 5x + 6x + 30)

= (1/2)(x² + 11x + 30)

Problem 15 :

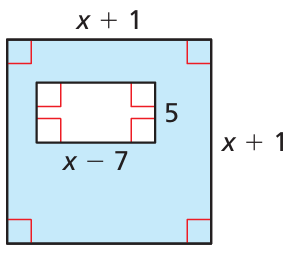
Solution :

By observing the figrue, we have rectangle inscribed in a square.

Dimensions of rectangle :

Length = x - 7 and width = 5

Dimensions of sqaure :

Side length = x + 1

Area of shaded region = Area of sqaure - area of rectangle

= (x + 1)(x + 1) - (x - 7) 5

= x² + 1x + 1x + 1 - 5x + 35

= x² + 2x - 5x + 35 + 1

= x² - 3x + 36