MULTIPLE REPRESENTATIONS OF RELATIONS

Express the relation as

i) set of ordered pairs

ii) Table

iii) Graph

iv) mapping diagram

Problem 1 :

In the scoring of some track meets, for 1^st place you get 5 points, for 2^nd place you get 3 points, for 3^rd place you get 2 points and for 4^th place you get 1 point.

Solution :

a)  Set of ordered pairs is

{(1, 5), (2, 3), (3, 2), (4, 1)}.

b) Table

c) Graph

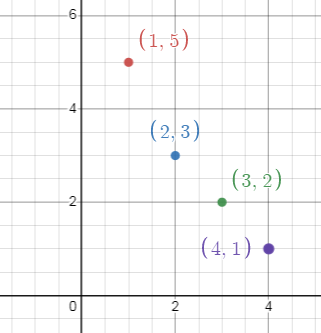
d) Mapping diagram :

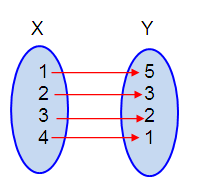
Problem 2 :

g(m) = m²

for the domain {-2, 0 2}

Solution :

If  m = -2

g(-2) = (-2)² = 4

If  m = 0

g(0) = (0)² = 0

If  m = 2

g(2) = (2)² = 4

a. Set of ordered pairs :

Set of ordered pairs is

{(-2, 4), (0, 0), (2, 4)}.

b. Table of values :

Graph :

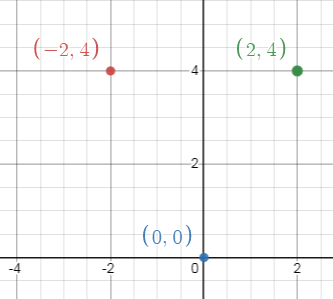
Mapping Diagram :

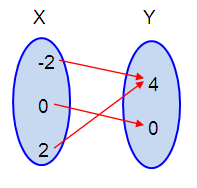
Problem 3 :

h(x) = -1/3x – 1

for the domain {-3, 0, 6}

Solution :

If  x = -3

h(-3) = (-1/3)(-3) – 1 = 0

If  x = 0

h(0) = (-1/3)(0) – 1 = -1

If  x = 6

h(6) = (-1/3)(6) – 1 = -3

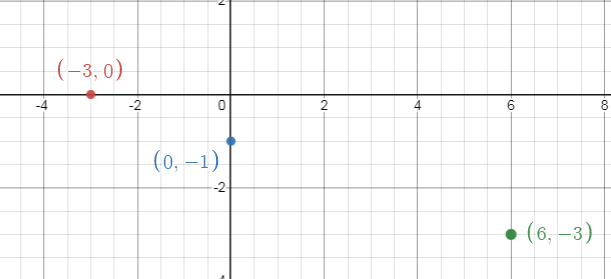
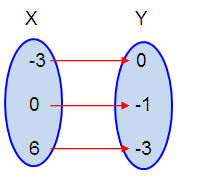
a. Set of ordered pairs :

Set of ordered pairs is

{(-3, 0), (0, -1), (6, -3)}.

b. Table of values :

Graph :

Mapping Diagram :

Problem 4 :

A tanning salon charges a one – time maintenance fee of $12 plus $4 for each tanning visit. Write a function to describe the situation. Find a reasonable domain and range for the function for up to 6 visits.

Solution :

Let x be a number of visits.

Let y be a total cost

y = 12 + 4x

0 ≤ x ≤ 6 and x should be an integer.

when, x = 6

y = 12 + 4(6)

y = 36

So, domain = {0, 1, 2, 3, 4, 5, 6}.

Range = {12, 16, 20, 24, 28, 32, 36}

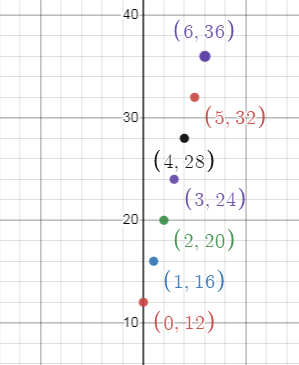
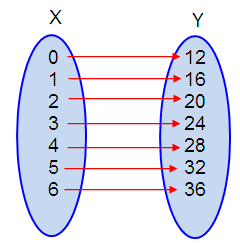
a. Set of ordered pairs :

{(0, 12), (1, 16), (2, 20), (3, 24), (4, 28), (5, 32), (6, 36)}.

Table :

Graph :

Mapping Diagram :

Problem 5 :

f(x) = x² + x – 2

for the domain {-2, 0 1}

Solution :

If x = -2

f(-2) = (-2)² + (-2) – 2

= 0

If x = 0

f(0) = (0)² + 0 – 2

= -2

If x = 1

f(1) = (1)² + 1 – 2

= 0

So, range of the function is {-2, 0}.

a. Set of ordered pairs :

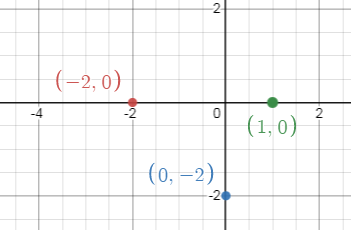
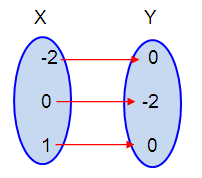
{(-2, 0), (0, -2), (1, 0)}.

b. Table :

c. Graph :

d. Mapping Diagram :