MODELLING QUADRATIC FUNCTIONS WORD PROBLEMS

Problem 1 :

Jason jumped off of a cliff into the ocean in Acapulco while vacationing with some friends. His height as a function of time could be modeled by the function

h(t) = -16t² + 16t + 480

where t is the time in seconds and h is the height in feet.

a. How long did it take for Jason to reach his maximum height?

b. What was the highest point that Jason reached?

c. What was Jason’s initial height?

Solution :

h(t) = -16t² + 16t + 480

a) To find maximum height, we have to write the given quadratic equation from standard form to vertex form.

Vertex is (1/2, 484). So, it will reach maximum height at 0.5 seconds.

b) Jason has reached 484 feet.

c)  To find the initial height, we have to apply t = 0

h(t) = 480 feet

So, the initial height is 480 feet.

Problem 2 :

If a toy rocket is launched vertically upward from ground level with an initial velocity of 128 feet per second, then its height h, after t seconds is given by the equation 

h(t) = -16t² + 128t

(air resistance is neglected)

a. How long will it take the rocket to hit its maximum height?

b. What is the maximum height?

c. How long did it take for the rocket to reach the ground?

Solution :

a)  h(t) = -16t² + 128t

h(t) = -16(t² - 8t)

= -16(t² - 2 x t x 4 + 4² - 4²)

= -16[(t - 4)² - 16]

= -16(t - 4)² + 256

Vertex of the parabola is (4, 256)

So, it is reaching the maximum height in 4 seconds.

b) Its maximum height is 256 feet.

c)  When it reaches the ground, its height will be 0.

-16t² + 128t = 0

-t² + 8t = 0

-t(t - 8) = 0

t = 0 and t = 8

So, it will reach the ground after 8 seconds.

Problem 3 :

You are trying to dunk a basketball. You need to jump 2.5 ft in the air to dunk the ball. The height that your feet are above the ground is given by the function.

h(t) = -16t² + 12t

What is the maximum height your feet will be above the ground?

Will you be able to dunk the basketball?

Solution :

h(t) = -16t² + 12t

To find its maximum height, we have to write the given in the vertex form.

x-coordinate of the vertex = -b/2a

Here a = -16, b = 12 and c = 0

x-coordinate = -12/2(-16)

= 3/8

= 0.375

No he will not able to dunk the basketball.

Problem 4 :

A ball is thrown in the air. The path of the ball is represented by the equation

h(t) = -t² + 8t

 Graph the equation over the interval 0 < t < 8.

Solution :

h(t) = -t² + 8t

To draw the graph of a quadratic function, we need the following 3 details.

i) Vertex

ii) x - intercept

iii) y - intercept

i)  Writing the given in vertex form :

h(t) = -[t² - 8t]

= -[t² - 2 x t x 4 + 4² - 4²]

= -[(t - 4)² - 16]

= -(t - 4)² + 16

Vertex of the parabola is (4, 16)

ii)  x - intercept :

h(t) = -t² + 8t

Put h(t) = 0

-t(t - 8) = 0

t = 0 and t = 8

iii) y-intercept :

Put t = 0

h(t) =  -0² + 8(0)

h(0) = 0

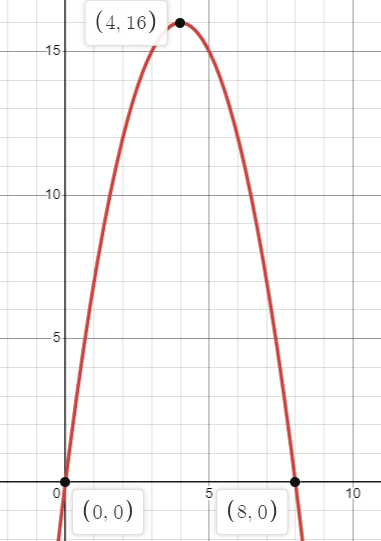
Problem 5 :

A small independent motion picture company determines the profit P for producing n DVD copies of a recent release is

P = -0.02n² + 3.40n - 16

P is the profit in thousands of dollars and n is in thousands of units.

a. How many DVDs should the company produce to maximize the profit?

b. What will the maximize profit be?

Solution :

P = -0.02n² + 3.40n - 16

Let us use the formula to find minimum or maximum value of the quadratic function.

a = -0.02, b = 3.40 and c = -16

i)  x-coordinate = -b/2a

= -3.40/2(-0.02)

= 3.40/0.04

= 85

So, the number of DVDs to be produced is 85.

ii)  To find the maximum profit, we have to find the value of y.

Here by applying n = 85, we will get the value of P and that is the maximum profit.

P = -0.02(85)² + 3.40(85) - 16

= -1.7 + 289 - 16

= 271.3

So, the maximum profit is $271.3