MIDSEGMENT THEOREM OF A TRAPEZOID

Example 1 :

In the figure, YZ is the midsegment of trapezoid TWRV.  Determine the value of x.

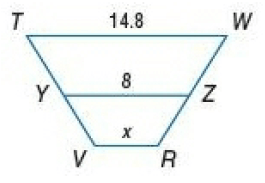
Solution :

Length of line segment YZ = length of (TW + VR)/2

8 = (14.8 + x)/2

8(2) = 14.8 + x

16 = 14.8 + x

x = 16 - 14.8

x = 1.2

So, length of line segment VR is 1.2

Example 2 :

Solve for x.

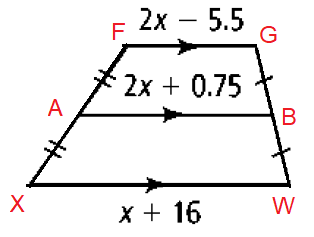
Solution :

2x + 0.75 = (2x - 5.5 + x + 16)/2

2x + 0.75 = (3x + 10.5)/2

2(2x + 0.75) = 3x + 10.5

4x + 1.5 = 3x + 10.5

Subtracting 3x and 1.5 on both sides.

4x - 3x = 10.5 - 1.5

x = 9

Example 3 :

Find the length of TU.

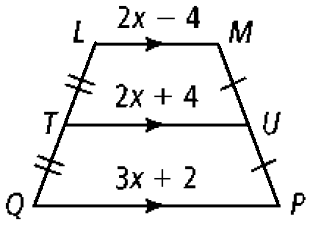
Solution :

TU = (LM + QP)/2

2x + 4 = (2x - 4 + 3x + 2)/2

2x + 4 = (5x - 2)/2

2(2x + 4) = 5x - 2

4x + 8 = 5x - 2

4x - 5x = -2 - 8

-x = -10

x = 10

TU = 2x + 4

TU = 2(10) + 4

TU = 20 + 4

TU = 24

Example 4 :

CD is the midsegment of trapezoid WXYZ.

a. What is the value of x?

b. What is XY?

c. What is WZ?

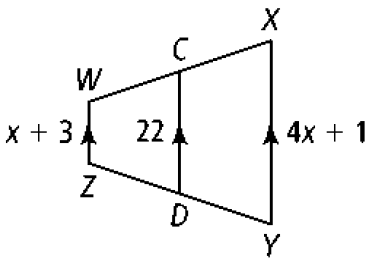
Solution :

CD = (WZ + XY)/2

22 = (x + 3 + 4x + 1)/2

44 = 5x + 4

40 = 5x 

x = 40/5

x = 8

a) The value of x is 8.