MIDPOINT AND DISTANCE IN THE COORDINATE PLANE

Problem 1 :

The point which lies on the perpendicular bisector of the line segment joining the points A(-2, -5) and B(2, 5) is

(A) (0, 0)    (B) (0, 2)    (C) (2, 0)    (D) (-2, 0)

Solution:

The perpendicular bisector is a perpendicular line passes through its midpoint .

Let P be the midpoint of line segment joining the points A and B.

So, the coordinates of P are given by the formula,

Hence, option (A) is correct.

Problem 2 :

The fourth vertex D of a parallelogram ABCD whose three vertices are A(-2, 3), B(6, 7) and C(8, 3) is

(A) (0, 1)    (B) (0, -1)    (C) (-1, 0)    (D) (1, 0)

Solution:

Let the fourth vertex D = (x, y)

Midpoint of two points (x₁, y₁) and (x₂, y₂) is calculated by the formula

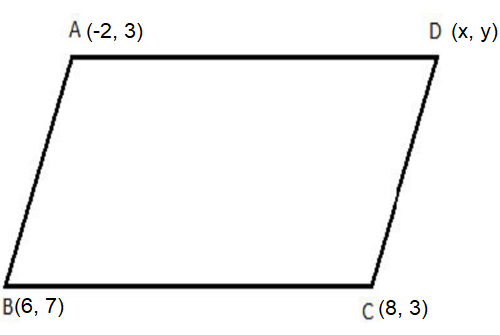
Hence, The point D is (0, -1).

So, option (B) is correct.

Problem 3 :

If P(a/3, 4) is the midpoint of the line segment joining the points Q(-6, 5) and R(-2, 3), then the value of a is

(A) -4     (B) -12     (C) 12     (D) -6

Solution:

So, option (B) is correct.

Problem 4 :

The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at

(A) (0, 13)  (B) (0, -13)  (C) (0, 12)  (D) (13, 0)

Solution:

The given points are A(x₁, y₁) = (1, 5) and B(x₂, y₂) = (4, 6)

The perpendicular bisector of AB will pass through the midpoint of AB.

Now, the perpendicular bisector of AB will meet y axis at P(0, y).

AP = BP

Applying distance formula, we get

AP² = BP²

(x₁ - 0)² + (y₁ - y)² = (x₂ - 0)² + (x₂ - y)²

(1 - 0)² + (5 - y)² = (4 - 0)² + (6 - y)²

1 + 25 + y² - 10y = 16 + 36 + y² - 12y

26 + y² - 10y = 52 + y² - 12y

26 - 2y = 0

-2y = -26

y = 13

Therefore, the perpendicular bisector of the line segment is (0, 13).

So, option (A) is correct.

Problem 5 :

The coordinates of the point which is equidistant from the three vertices of the Δ AOB.

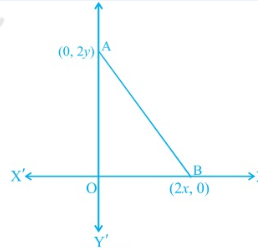
(A) (x, y)   (B) (y, x)   (C) x/2, y/2   (D) y/2, x/2

Solution:

Let the coordinate of the point which is equidistant from the three vertices O(0, 0), A(0, 2y) and B(2x, 0) is P(h, k).

Then, PO = PA = PB

By distance formula,

Taking first two equations, we get

h² + k² = h² + (k - 2y)²

k² = k² + 4y² - 4yk

4y(y - k) = 0

y = k

Taking first and third equations, we get

h² + k² = (h - 2x)² + k²

h² = h² + 4x² - 4xh

4x(x - h) = 0

x = h

Therefore, required points = (h, k) = (x, y)

So, option (A) is correct.

Problem 6 :

A circle drawn with origin as the centre passes through (13/2, 0). The point which does not lie in the interior of the circle is

(A) (-3/4, 1)     (B) (2, 7/3)

(C) (5, -1/2)     (D) (-6, 5/2)

Solution:

Radius of the circle = Distance between the two points

A point lies inside, on or outside the circle if the distance of the point from the centre of the circle is less than, equal to or greater than the radius of the circle.

a) The distance between (0, 0) and (-3/4, 1)

So, the point (-3/4, 1) lies in the interior of the circle.

b)  The distance between (0, 0) and (2, 7/3)

So, the  point (2, 7/3) lies in the interior of the circle.

C)  The distance between (0, 0) and (5, -1/2)

So, the point (5, -1/2) lies in the interior of the circle.

D)  The distance between (0, 0) and (-6, 5/2)

Therefore, the point (-6, 5/2) lies on the circle.

So, option (D) is correct.

Problem 7 :

A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are respectively 

(A) (0, -5) and (2, 0)    (B) (0, 10) and (-4, 0)

(C) (0, 4) and (-10, 0)   (D) (0, -10) and (4, 0)

Solution:

Let the coordinates of P be (x, y) and Q be (x₂, y₂)

Midpoint of PQ = (2, -5)

By midpoint formula,

Since line PQ intersects the y axis at P.

So, x₁ = 0, y₂ = 0

0 + x₂ = 4

x₂ = 4

y₁ + 0 = -10

y₁ = -10

The coordinates of P is (0, -10) and Q is (4, 0).

So, option (D) is correct.

Problem 8 :

If the distance between the points (4, p) and (1, 0) is 5, then the value of p is

(A) 4 only     (B) ± 4     (C) -4 only     (D) 0

Solution:

The given points are (1, 0) and (4, p)

So, option (B) is correct.