MEASURING ANGLE IN THE COORDINATE PLANE

We can think about the coordinate plane in terms of direction. 

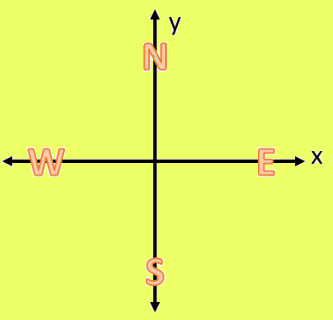
Starting from the x-axis, there are two types of rotations. 

(i) Clockwise

(ii) Anticlockwise

θ is positive for anticlockwise rotations and negative for clockwise rotations.

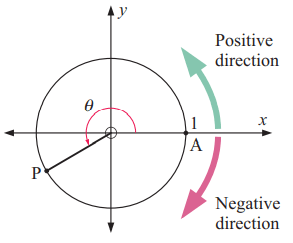
Find the measure of each angle.

Problem 1 :

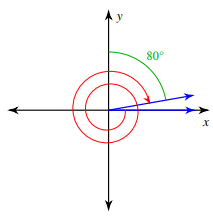
Solution :

Angle is rotated in clockwise rotation. Angle created during the rotation

= -(360 + 360 - 10)°

= -(720 - 10)°

= -710°

Problem 2 :

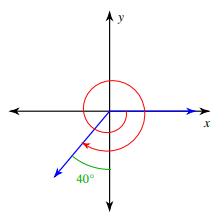
Solution :

Angle is rotated in clockwise rotation. Angle created during the rotation

= -(360 + 90 + 40)°

= -490°

Problem 3 :

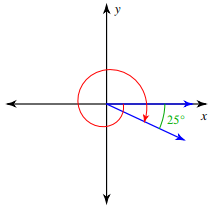
Solution :

Angle is rotated in clockwise rotation. Angle created during the rotation

= -(360 + 25)°

= -385°

Problem 4 :

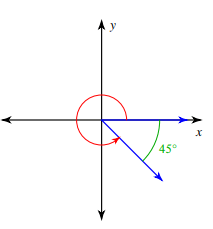
Solution :

Angle is rotated in anticlockwise rotation. Angle created during the rotation

= (360 - 25)°

= 315°

Problem 5 :

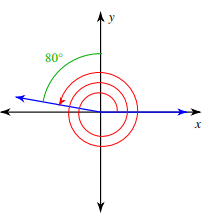
Solution :

Angle is rotated in anticlockwise rotation. Angle created during the rotation

= (360 + 360 + 90 + 80)°

= 890°

Problem 6 :

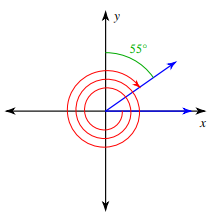
Solution :

Angle is rotated in clockwise rotation. Angle created during the rotation

= -(360 + 360 + 270 + 55)°

= -1045°

Problem 7 :

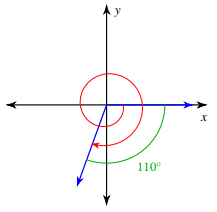
Solution :

Angle is rotated in clockwise rotation. Angle created during the rotation

= -(360 + 110)°

= -470°

Problem 8 :

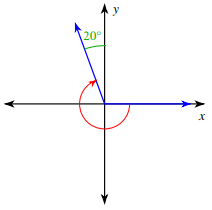
Solution :

Angle is rotated in clockwise rotation. Angle created during the rotation

= -(180 + 90 - 20)°

= -250°

Problem 9 :

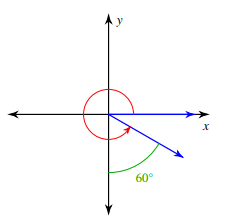
Solution :

Angle is rotated in anticlockwise rotation. Angle created during the rotation

= (270 + 60)°

= 330°

Problem 10 :

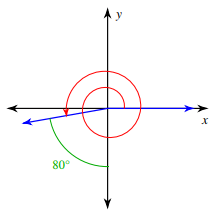
Solution :

Angle is rotated in anticlockwise rotation. Angle created during the rotation

= (360 + 180 + 90 - 80)°

= 550°