MEAN VALUE THEOREM FOR INTEGRALS WORKSHEET

For each problem, find the values of c that satisfy the Mean Value Theorem for Integrals.

Problem 1 :

Solution

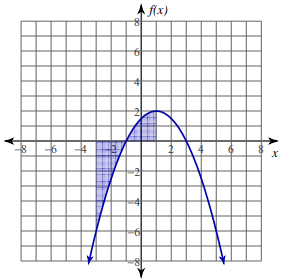
Problem 2 :

f(x) = 4/x² ; [-4, -2]

Solution

For each problem, find the average value of the function over the given interval. Then, find the values of c that satisfy the Mean Value Theorem for Integrals.

Problem 3 :

f(x) = −x + 2; [−2, 2]

Solution

Problem 4 :

Solution

Problem 5 :

Solution

Problem 6 :

Solution