MEAN VALUE THEOREM FOR INTEGRALS EXAMPLES

If f is continuous on [a, b], then at some point c in [a, b],

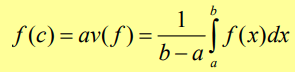
The graphical rectangular interpretation of the Mean value theorem for Definite Integrals is that:

If f is continuous on [a, b], then at some point c in [a, b] there is a rectangle with height f(c), and length b – a, such as the area of the rectangle equals the area under the curve f(x) on the interval [a, b]

For each problem, find the values of c that satisfy the Mean Value Theorem for Integrals.

Problem 1 :

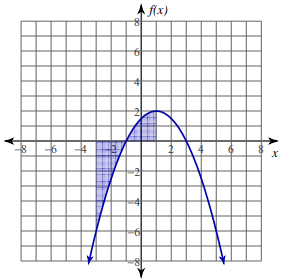
Solution :

Equating the value derived from mean value theorem for integrals to f(x), we get

Problem 2 :

f(x) = 4/x² ; [-4, -2]

Solution :

Here a = -4, b = -2

Equating the value derived from mean value theorem for integrals to f(x), we get

For each problem, find the average value of the function over the given interval. Then, find the values of c that satisfy the Mean Value Theorem for Integrals.

Problem 3 :

f(x) = −x + 2; [−2, 2]

Solution :

Finding average value of the function :

Finding the value of c that lies in the given interval :

So, the value of c is 0, which lies in the interval.

Problem 4 :

Solution :

Finding average value of the function :

Finding the value of c, using mean value theorem :

So, the value of c is 3.8, which lies in the interval.

Problem 5 :

Solution :

Finding average value of the function :

Finding the value of c, using mean value theorem :

Problem 6 :

Solution :

Finding average value of the function :

Finding the value of c, using mean value theorem :

MEAN VALUE THEOREM FOR INTEGRALS EXAMPLES

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling