MATCHING THE GRAPH OF SQUARE ROOT FUNCTION AND THE EQUATION

To match the graph of square root function, we have to analyze the following.

1) If there is any horizontal or vertical stretch or shrink

2) If there is any horizontal or vertical translation of the curve.

3) We have to remember the graph of the parent function of square root function.

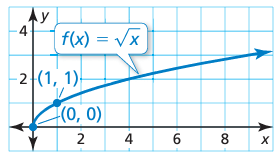
The square root function will be in the form

y = a√b(x - h) + k

To fix the values of a and b, we have to choose two points randomly from the given graph and figure out the values of a and b.

Problem 1 :

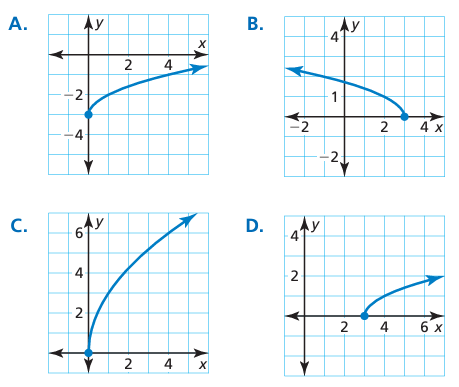
Match the function and its graph. Describe the range.

1) y = √(x - 3)               2)  3√x

3)  y = √x - 3               4)  y = √(-x + 3)

Solution :

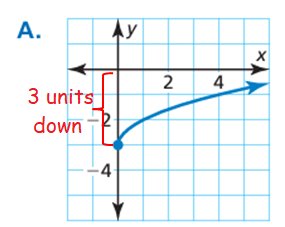
Graph A :

There is vertical translation of 3 units down, here is no horizontal translation.

y = √x - 3

So, question (3) matches with Graph A.

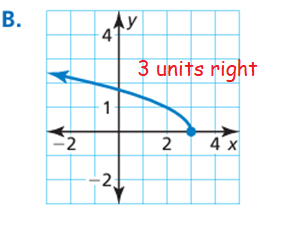
Graph B :

Seems there is reflection across y-axis. 

y = √(-x + 3)

y = √-(x - 3)

Moving the graph 3 units.

So, question (4) matches with Graph B.

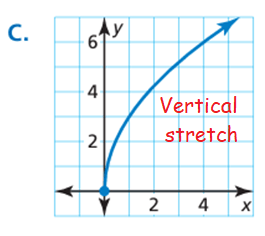
Graph C :

There is vertical stretch of 3 units.

y = 3√x

Applying the point (4, 6)

6 = 3√4

6 = 3(2)

6 = 6

So, question (2) matches with Graph C.

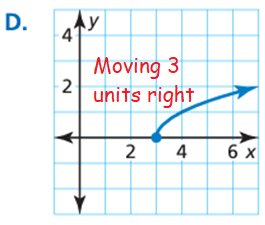
Graph D :

There is no stretch, there is horizontal move of 3 units.

y = √(x - 3)

So, question (1) matches with Graph D.

Problem 2 :

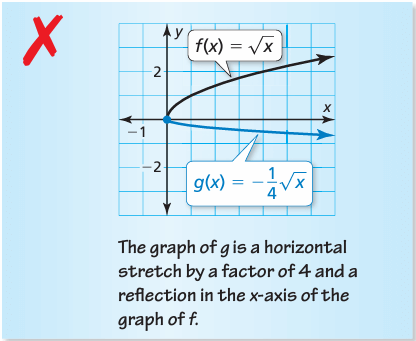
Describe and correct the error in comparing the graph of

g(x) = −(1/4)√x

to the graph of

f(x) = √x

Solution :

Comparing the given function g(x) = −(1/4)√x, a = 1/4. 

The value of a will decide whether it is vertical stretch or shrink. 0 < a < 1, then it is vertical shrink. Since the sign of a is negative, it is the reflection across x-axis. 

So, the error is instead of representing vertical shrink, it is said as horizontal stretch.

Problem 3 :

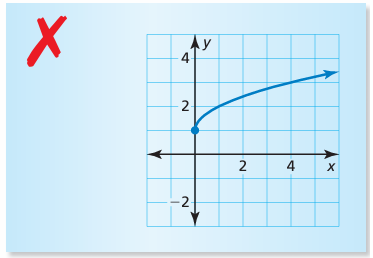
Describe and correct the error in graphing the function

y = √(x + 1)

Solution :

y = √(x + 1)

y = √(x - (-1))

Comparing the given function with standard form, the value of h is -1. So, we have to move the graph 1 unit towards the left.

The error is, in the graph shown the graph is move up 1 unit instead of moving left 1 unit.

Problem 4 :

The graph represents the function f (x) = √x .

a. What is the minimum value of the function?

b. Does the function have a maximum value? Explain.

c. Write a square root function that has a minimum value of −4.

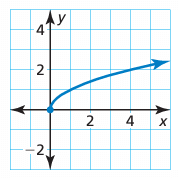
Solution :

f (x) = √x

a) By observing the graph, the minimum value of the function is (1, 0).

b) The function f(x) will not have maximum value.

c)  Comparing the given function with f (x) = a√ b(x - h) + k

The square root function which has -4 as the minimum value will be

f (x) = √(x - (-4))

Then, the required function will be

f (x) = √(x + 4)