MATCHING GRAPHS OF FUNCTIONS AND THEIR DERIVATIVES WORKSHEET
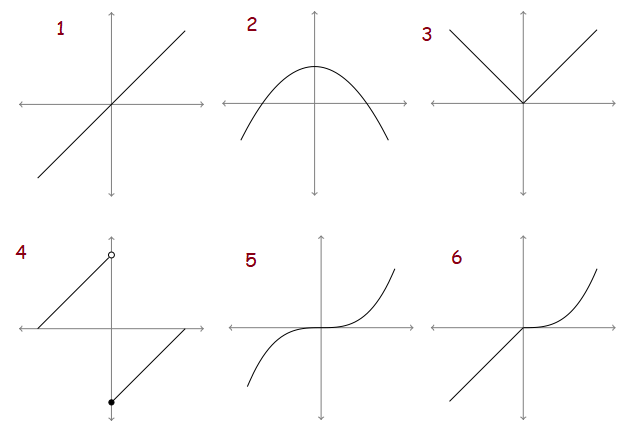
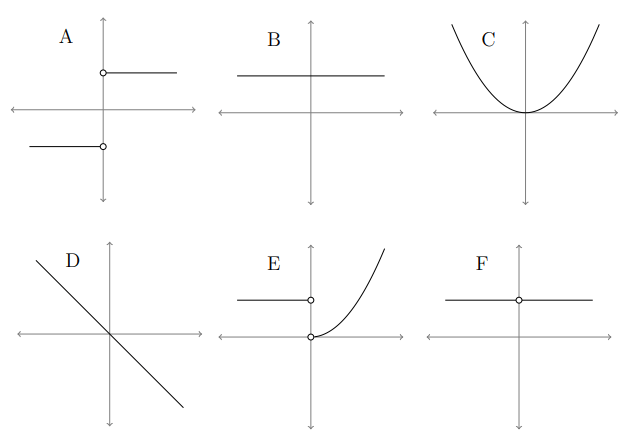
Six graphs of functions are below, along with six graphs of derivatives. Match the graph of each function with the graph of its derivative
Questions :
Derivative graph
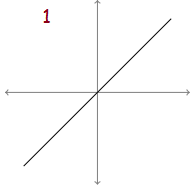
Problem 1 :
Solution :
The graph is a raising line, it will represent the function in the form ax + by + c = 0
While finding the derivative of the function, dy/dx = constant
Graphical form of the derivative must be a horizontal line.
|
Original function  |
Derivative 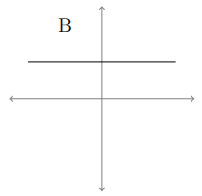 |
Problem 2 :
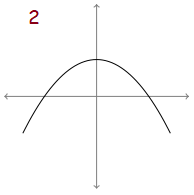
Solution :
The graph of original function is parabola. It must be in the form of y = x2
Its derivative will be dy/dx = 2x
By analyzing the graph of original function,
- In (-∞, 0), the original function is increasing, then in the derivative graph should be above the x-axis in this interval.
- (0, ∞), the original function is decreasing, then in the derivative graph should be below the x-axis in this interval.
|
Original function  |
Derivative function  |
Problem 3 :
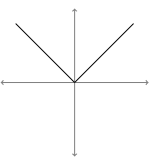
Solution :
The graph of original function is absolute value function. It must be in the form of y = a|x - h| + k
Derivative of absolute value function,
y' = a(x - h) / |x - h|
On x = h, there is a hole.
- In (-∞, 0), the original function is decreasing function
- In (0, ∞), the original function is increasing.
- At x = 0, we have sharp edge, so derivative is not defined at x = 0
|
Original function  |
Derivative function 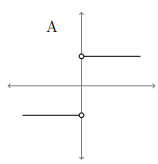 |
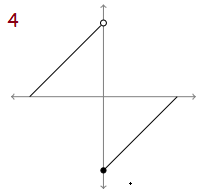
Problem 4 :
Solution :
Lim x --> 0- f(x) ≠ Lim x --> 0+
Then the derivative is not defined at x = 0. Since the original function is raising and falling line, its derivative graph must be horizontal line.
|
Original function  |
Derivative function 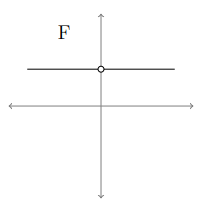 |
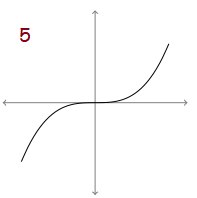
Problem 5 :
Solution :
The graph of the original function is looks like a graph of cubic function. Then its derivative graph must be a graph of quadratic function. By observing the graph more clearly, it is increasing function. So, the entire derivative graph must be above the x-axis.
|
Original function  |
Derivative function 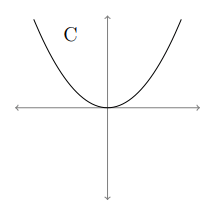 |
Problem 6 :
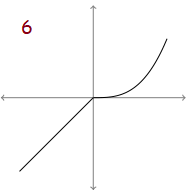
Solution :
By observing the graph, there are two pieces and at x = 0 we have sharp edge.
At x = 0, the derivative is not defined and the original graph is increasing entirely. Then its derivative graph must be above the x-axis.
|
Original function  |
Derivative function 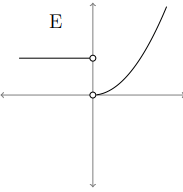 |
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling