MATCHING GRAPH OF QUADRATIC FUNCTION AND EQUATION

Match each equation with its graph, then find the domain and range of each function.

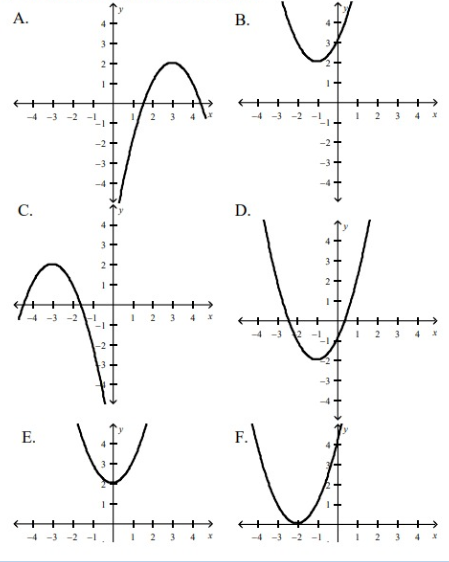
Problem 1 :

f(x) = (x + 2)²

D: ____  R: _____

Problem 2 :

f(x) = -(x + 3)² + 2

D: ____ R: ____

Problem 3:

f(x) = -(x - 3)² + 2

D: ____ R: ____

Problem 4 :

f(x) = (x + 1)² + 2

D: ____ R: ____

Problem 5 :

f(x) = (x + 1)² - 2

D: ____ R: ____

Problem 6 :

f(x) = x² + 2

D: ____ R: ____

Problem 1 :

f(x) = (x + 2)²

D: ____  R: _____

Solution:

f(x) = (x + 2)²

Comparing the given function with 

y = a(x - h)² + k

Direction of opening : 

Since the value of a is positive, the parabola opens up.

Vertex of the parabola :

(h, k) = (-2, 0)

Matching the graph :

Comparing with the parent function, y = x², the graph should be moved horizontally left of 2 units.

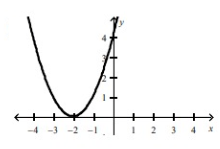
The graph representing the function f(x) = (x + 2)² is option F.

Domain:

All real numbers

Range:

y > 0

Problem 2 :

f(x) = -(x + 3)² + 2

D: ____ R: ____

Solution:

f(x) = -(x + 3)² + 2

Direction of opening : 

Since the value of a is negative, the parabola opens down.

Vertex of the parabola :

(h, k) = (-3, 2)

Matching the graph :

Comparing with the parent function, y = x², moving left 3 units and moving up 2 units.

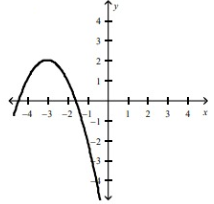
The graph representing the function f(x) = -(x + 3)² + 2 is option C.

Domain:

All real numbers

Range:

y < 2

Problem 3:

f(x) = -(x - 3)² + 2

D: ____ R: ____

Solution:

f(x) = -(x - 3)² + 2

vertex (h, k) = (3, 2)

Direction of opening : 

Since the value of a is negative, the parabola opens down.

Vertex of the parabola :

(h, k) = (3, 2)

Matching the graph :

Comparing with the parent function, y = x², reflection across x-axis moving right 3 units and moving up 2 units.

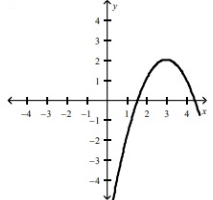
The graph representing the function f(x) = -(x - 3)² + 2 is option A.

Domain:

All real numbers

Range:

y < 2

Problem 4 :

f(x) = (x + 1)² + 2

D: ____ R: ____

Solution:

f(x) = (x + 1)² + 2

Direction of opening : 

Since the value of a is positive, the parabola opens up.

Vertex of the parabola :

(h, k) = (-1, 2)

Matching the graph :

Comparing with the parent function, y = x², horizontally moving right 3 units and moving up 2 units.

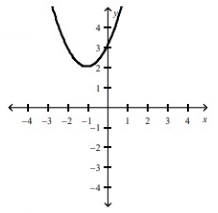
The graph representing the function f(x) = -(x - 3)² + 2 is option B.

Domain:

All real numbers

Range:

y > 2

Problem 5 :

f(x) = (x + 1)² - 2

D: ____ R: ____

Solution:

f(x) = (x + 1)² - 2

Direction of opening : 

Since the value of a is positive, the parabola opens up.

Vertex of the parabola :

(h, k) = (-1, -2)

Matching the graph :

Comparing with the parent function, y = x², moving the graph horizontally left 1 unit and down 2 units.

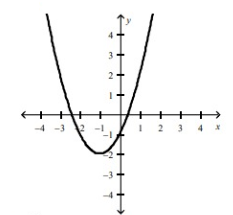
The graph representing the function f(x) = (x + 1)² - 2 is option D.

Domain:

All real numbers

Range:

y > -2

Problem 6 :

f(x) = x² + 2

D: ____ R: ____

Solution:

f(x) = x² + 2

Direction of opening : 

Since the value of a is positive, the parabola opens up.

Vertex of the parabola :

(h, k) = (0, 2)

Matching the graph :

Comparing with the parent function, y = x², moving the graph vertically 2 units up.

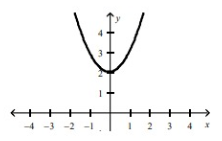
The graph representing the function f(x) = x² + 2 is option E.

Domain:

All real numbers

Range:

y > 2