MATCH THE SYSTEM OF INEQUALITIES WITH ITS GRAPH

Problem 1 :

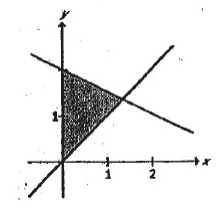
Match the graph with the correct system of inequalities.

E) None of these

Solution:

Let take the point (0.5, 1).

To check the given inequalities,

So, option (A) is correct.

Problem 2 :

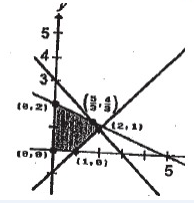
Find the maximum of the objective function: Z = 9x + 6y given the following constraints:

x + y ≤ 3

x - y ≤ 1

2x + 5y ≤ 10

x ≥ 0

y ≥ 0

A) 9     B) 12     C) 24     D) 36     E) None of these

Solution:

To find the maximum value of the function Z = 9x + 6y

we have to apply the corner points, one by one in the function Z = 9x + 6y.

(0, 0) (0, 2) (1, 0) (2, 1)(5/3, 4/3)

Applying the point (5/3, 4/3)

Z = 9x + 6y

Z = 9(5/3) + 6(4/3)  ==> 15+8 ==> 23

So, the maximum value is 24, option C.

Problem 3 :

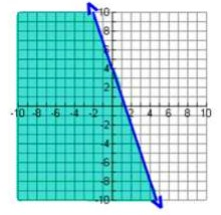
Which inequality represents the graph to the right?

a) y ≥ 3x + 4          b) y ≤ -3x + 4          c) y > -3x + 4

d) y < 3x + 4

Solution:

It is easy to choose two point from the given picture.

(0, 4) and (1, 1)

Slope m = (1 - 4)/(1-0)

m = -3

Since it is falling line, it has negative slope. It is solid line, then we have to choose ≥ or ≤.

Let take the point (-2, 2).

To check given inequalities

a)

y ≥ 3x + 4

2 ≥ 3(-2) + 4

2 ≥ -6 + 4

2 ≥ -2 (False)

b)

y ≤ -3x + 4

2 ≤ -3(-2) + 4

2 ≤ 6 + 4

2 ≤ 10 (True)

So, option (b) is correct.

Problem 4 :

Which inequality represents the graph below?

a) y ≤ -3    b) y > -3     c) x > -3        d) x ≤ -3

Solution:

Let take the point (2, -4). Since it is vertical line, its equation will be x = a. accordingly the given options, checking with options a and b is useless.

To check given inequalities

c)

x > -3

2 > -3 (True)

d)

x ≤ -3

2 ≤ -3 (False)

So, option (C) is correct.

Problem 5 :

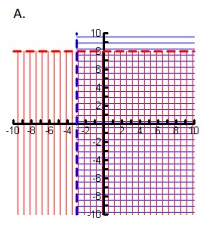
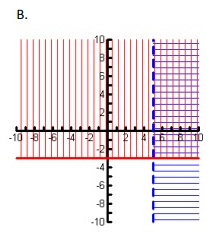
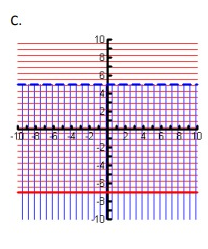
Match each system of equations to its graph below.

a) y < 8       x > -3

b) y < 5       y ≥ -7

c) y ≥ -3     x > 5

Solution:

a)

y < 8

x > -3

b)

y ≥ -3

x > 5

c)

y < 5

y ≥ -7

Problem 6 :

Which point is a solution to the system graphed to the right?

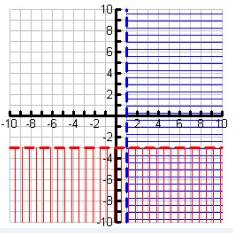
a) (4, 4)     b) (4, -4)      c) (-4, -4)     d) (-4, 4)

Solution:

Point (4, -4) in the shaded area.

The solution is (4, -4).

So, option (b) is correct.

Problem 7 :

Which point(s) are solution to the system graphed to the right?

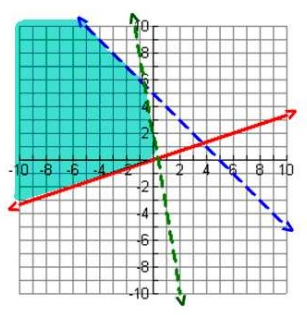
A) (-2, -3)       B) (-1, 1)       C) (2, 1)        D) (-4, 0)

Solution:

Point (-2, -3) and (2, 1) are not in the shaded area. Points (-1, 1) and (-4, 0) are in the shaded area.

So, option (B) and (D) is correct.